Testing important industrial problems with Honeywell’s Ion-Trap quantum computer — Calculating transition amplitudes of Azobenzene isomers using Honeywell System Model HØ

Figure 1. A photograph of Honeywell’s trapped-ion based quantum computing system. [source]

In June 2020, Honeywell became the first to commercially offer a quantum computer achieving a Quantum Volume of 64, with the launch of their System Model HØ. Following Honeywell’s announcement, we at QunaSys started thinking about what we could do with the world’s most powerful quantum computer?

In cooperation with Honeywell, we designed an experiment to calculate the photochemical response of an organic molecule, namely azobenzene, using the 6-qubit Honeywell quantum computer System Model HØ, as shown in Figure 1. Our results show a much higher level of accuracy than a typical superconducting quantum computer. The details of the results are as follows.

Oscillator strength of azobenzene

The most interesting property of azobenzene is the isomerization between trans- and cis- isomers, which can be switched by light. Based on this photo switch mechanism, azobenzene compounds are expected to have various applications, such as photopatterning, data storage, microfluid control, and drug release.

Figure 2. The transition between the isomers of azobenzene is controlled by light response, which can be calculated by oscillator strength.

Generally when a molecule is irradiated by light, its electrons transition from the ground state to a higher energy state as a consequence, with some probability. The oscillator strength is the key physical property in determining this probability. We can use this property to calculate the population of excited states, which can then be used to evaluate the likelihood of the isomerization. Calculating the oscillator strength requires a quantum computer to have high accuracy since it needs to prepare superpositions of multiple energy-eigenstates, even if we use a proprietary hardware-friendly method (see the last section for details). Therefore, calculating the oscillator strength is an ideal test for Honeywell’s 6-qubit device that is experimentally simultaneously challenging and of practical importance. In the experiment, we calculated the oscillator strength of azobenzene using the hardware and compared the results with the exact classical simulation.

Experiment

We calculated the oscillator strength between two energy eigenstates of cis-azobenzene, using the subspace-search variational quantum eigensolver (SSVQE), proposed by QunaSys Inc. For a detailed description of the overall experimental setup, please see the last section.

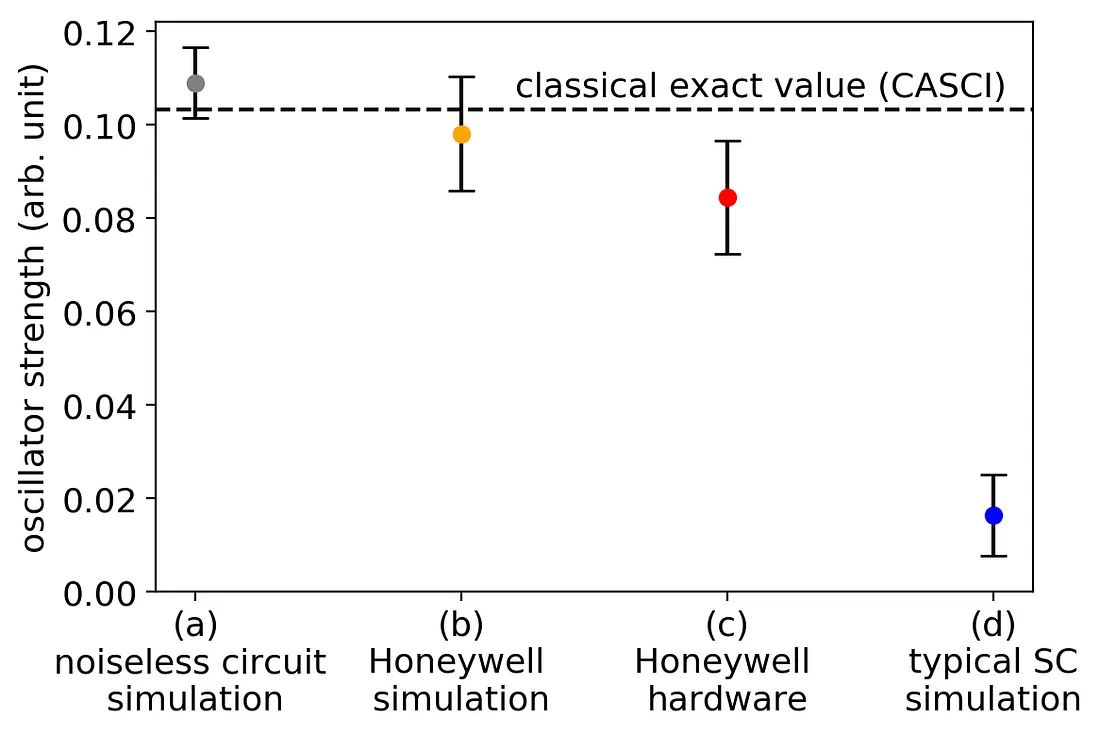
Figure 3. Calculated oscillator strengths of an azobenzene molecule. The horizontal dashed line indicates the exact value from the classical CASCI (complete active space configuration interaction) method, for which we are aiming. Each dot (a)-(d) shows the value of oscillator strength computed with either classical circuit simulations or the Honeywell’s hardware, using an identical quantum circuit. (a) Classical simulation result assuming a noise-free quantum computer. (b) A classical simulation which mimics Honeywell’s hardware. (c) The calculation result of Honeywell’s real hardware. (d) A classical simulation that mimics typical superconducting quantum hardware currently available on a cloud service. The error bars were calculated using the definition of the oscillator strength and the results of the 500 shots measurements from classical circuit simulations or the Honeywell’s hardware.

Figure 3 shows the calculation result of the oscillator strength of azobenzene. As evident in the figure, the value from Honeywell’s hardware (red dot) is much closer to the exact value (horizontal dashed line) we are aiming for than the simulation result based on the noise level of a typical superconducting quantum computer (blue dot). These results indicated that the fidelities of gate operations are of essential importance when calculating more complex physical quantities.

Conclusion

We used Honeywell’s 6-qubit trapped-ion quantum computer with Quantum Volume 64 to calculate the oscillator strength of the azobenzene molecule. The accuracy of the results obtained on Honeywell’s quantum computer is much higher than those achieved through a simulation on a typical superconducting quantum computer. By combining Honeywell’s ultra-high-precision hardware and the SSVQE algorithm, we successfully calculate this important quantity with high accuracy, expanding the horizon of quantum computers’ applications. Although some have questioned the ability of trapped-ion systems to scale, the QCCD architecture realized by Honeywell has the potential to solve these bottlenecks. Honeywell has already announced a new release of a next generation system with a Quantum Volume of 128. We’re looking forward to the future of this technology which we believe will accelerate industrial applications of trapped-ion quantum computers.

Details of simulation setup

We use the subspace-search variational quantum eigensolver (SSVQE), which we proposed in [Phys. Rev. Research, 1, 033062 (2019)], in this project. The SSVQE is an extension of the variational quantum eigensolver (VQE) and finds low-lying excited states of a given Hamiltonian by optimizing a parametrized unitary $U(θ)$ so that

U(\theta)\ket{a_j}\simeq \ket{\psi_j},

where $\{\ket{a_j}\}_{j=0,\dots,k-1}$ is the $j$ -th excited state of the Hamiltonian. As the optimization step needs many iterations to converge, we perform the optimization on a classical computer in this project. This may be avoided by using more sophisticated optimization techniques such as stochastic gradient descent which require less samples to optimize but due to time limitations, we circumvent possible trial-and-error in this step.

We use an electronic Hamiltonian of cis-azobenzene molecule, which becomes a 6-qubit Hamiltonian under an appropriate active space approximation. With this Hamiltonian, we evaluate the oscillator strength, which is proportional to a sum of the absolute square of transition amplitude $\bra{\psi_0}\mu_\alpha \ket{\psi_1}$ , where $\mu_\alpha (\alpha=x,y,z)$ is a dipole moment operator between the ground state and the first singlet excited state (note: this value vanishes for trans-azobenzene due to molecular symmetry).

Using the optimized unitary, we evaluate $\bra{\psi_0}\mu_\alpha \ket{\psi_1}$ by the following “virtual interference” technique. First, we prepare

\ket{\pm}=\frac{\ket{\psi_0}\pm \ket{\psi_1}}{\sqrt{2}}=U(\theta)\left(\frac{\ket{a_0}\pm \ket{a_1}}{\sqrt{2}}\right)

and

\ket{\pm i}=\frac{\ket{\psi_0}\pm i\ket{\psi_1}}{\sqrt{2}}=U(\theta)\left(\frac{\ket{a_0}\pm i\ket{a_1}}{\sqrt{2}}\right).

Second, we measure

\bra{+}\mu_{\alpha}\ket{+}, \bra{-}\mu_{\alpha}\ket{-}, \bra{+i}\mu_{\alpha}\ket{+i}, \text{and} \bra{-i}\mu_\alpha\ket{-i}.

Finally, we obtain $\bra{\psi_0}\mu_\alpha \ket{\psi_1}$ by classically computing the following:

2 \mathrm{Re}[\bra{\psi_0}\mu_\alpha \ket{\psi_1}]=\bra{+}\mu_{\alpha}\ket{+}-\bra{-}\mu_{\alpha}\ket{-},\\ 2 \mathrm{Im}[\bra{\psi_0}\mu_\alpha \ket{\psi_1}]=\bra{+i}\mu_{\alpha}\ket{+i}-\bra{-i}\mu_\alpha\ket{-i}.

Further, to mitigate hardware errors, we employed a linear extrapolation technique.

Written by

Yohei Ibe and Tennin Yan at QunaSys Inc.

(We deeply acknowledge helpful feedbacks from Honeywell's team)

QunaSys keeps developing efficient quantum algorithms to accelerate various applications of quantum computers. Our mission is to enthusiastically develop technologies that bring out the maximum potential of quantum computers and to continually deliver innovations to society.