While classical computers have bits representing either 0 or 1 values, quantum computers have qubits which provide arbitrary superposition of the bases and of quantum states. This intrinsic difference forms the powerfulness of quantum computers overwhelming classical computers. Though the quantum computer’s full potential is still in progress, we are now in the first stage where the so-called NISQ (Noisy Intermediate-Scale Quantum) devices are available. NISQ devices can operate only the limited number of algorithms for quantum computers, or quantum algorithms, because the error in their qubits prevents us from executing the complicated quantum algorithms. In the coming 3–5 years, we will need efficient quantum algorithms to explore the quantum advantage with NISQ devices having 50 to a few hundred qubits.
One of the most practical applications of quantum computers is expected to happen in quantum chemistry. This is because simulating molecules based on quantum mechanics requires exponential computational resources with increasing the number of atoms in molecules on classical computers, whereas it does polynomial on quantum computers. In particular, an algorithm called variational quantum eigensolver (VQE) [1] was designed to find energies of a target molecule and has shown its potential to run on real NISQ devices.
The VQE enables us to calculate electronic energies of molecules. When analyzing molecules in quantum chemistry, however, the derivatives of the energies with respect to some parameters defining the system are also essential. For example, the derivative with respect to the nuclear coordinates of the molecules gives the force acted on them. The force is utilized in various ways, such as determining the most stable molecular structure, elucidating chemical reaction paths, and performing molecular dynamics simulations. Another example is the derivative with respect to the external electric or magnetic fields, which tells us the spectroscopic properties of the molecules when they are irradiated by light.
There are two ways to obtain the energy derivatives in quantum chemistry. One is to use the finite-difference method, where we compute the derivatives at two proximate points and calculate the difference numerically. The other is the analytical approach, where we employ some analytical formulas for the derivative. The former is always applicable without any prior knowledge of the method to calculate the energies but vulnerable to the noise in the calculated energies. Since NISQ devices contain inevitable noises in their outputs, the analytical method is more practical in the current quantum age.
In 2019, two groups independently proposed methods to calculate analytical energy derivatives based on the VQE and applicable to NISQ device [2,3]. One was from Kosuke Mitarai (assistant professor at Osaka University & CSO at QunaSys Inc.), Yuya O. Nakagawa (lead researcher at QunaSys Inc.), and Wataru Mizukami (associate professor at Osaka University) in Japan [2]. They showed analytical formulas to calculate the derivatives of the energy obtained by the VQE, up to the third-order derivatives. They explicitly provided quantum circuits and ways of measurements to determine the quantities appearing in those formulas. All procedures in the proposed method require shallow (not-complicated) quantum circuits and are expected to be feasible on real NISQ devices. It is worthwhile to note that the proposed method can be applied to the derivative of excited-state energy, which is more difficult to calculate with classical computers.
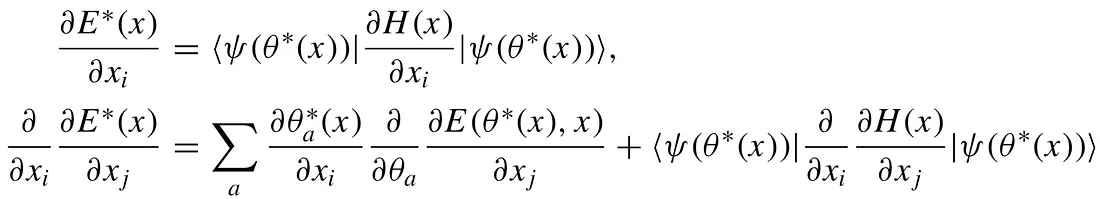
Main formulas for the first-order and second-order derivatives in [2]. All quantities in the formulas can be obtained by running quantum circuits and measuring qubits on NISQ devices.
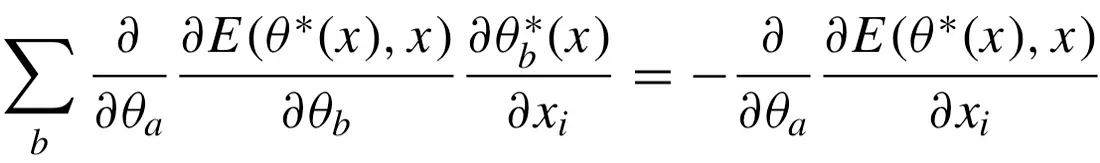
Equation which determines the quantity appearing in the formula for the second-order derivative above.
On the other hand, Tom O’Brien at Leiden University (currently also at Google Inc.) and his colleagues proposed a different method to evaluate the analytical energy derivatives on quantum computers [3]. The formula for the first-order derivative is the same as the method in Mitarai’s work, but the formulas for the second- and higher-order derivatives are based on the so-called sum-over-state approach that requires transition amplitudes involving all excited states in the system. In practice, the summation over all the excited states is truncated at the finite number of the states, and the error is introduced in the formals in a rigorous sense. Compared with Mitarai’s proposal, O’Brien’s work does not suffer from the classical computational cost related to the number of circuit-parameters used for the VQE, with a trade-off to the necessity to calculate the excited states even for evaluating the derivatives of the ground-state energy. In addition to the theoretical proposal, the authors of [3] did an experiment to calculate the first-order derivate of energy with respect to the nuclear displacements on a two-qubit superconducting device and illustrated they could perform the geometry optimization of hydrogen molecule based on that derivative.
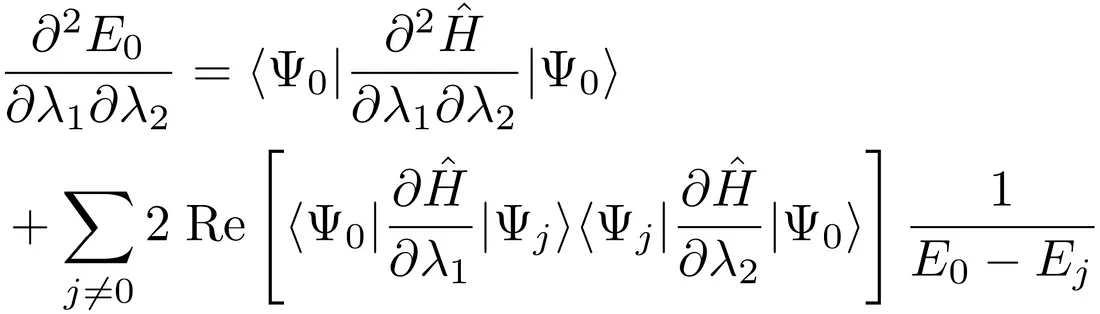
Main formula for the second-order derivative in [3]. The formula for the first-order derivative is the same as [2]. represents the energy level and runs all excited states.
The energy derivatives are universally used in the calculation of the properties of molecules. The proposals explained in this blog post open up the further possibility to take advantage of NISQ devices as we approach the quantum-computer era. With the simultaneous development of the hardware of quantum computers and new quantum algorithms to exploit them, we are looking forward to more and more practical applications of quantum computers to calculations in quantum chemistry, which would eventually outperform classical computers.
References
[1] A. Peruzzo, J. McClean, P. Shadbolt, M.-H Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’Brien. “A variational eigenvalue solver on a photonic quantum processor.” Nat. Commun. 5, 4213 (2014). [link]
[2] K. Mitarai, Y. O. Nakagawa, and W. Mizukami. “Theory of analytical energy derivatives for the variational quantum eigensolver.” Phys. Rev. Research 2, 013129 (2020). [link]
[3] T. E. O’Brien, B. Senjean, R. Sagastizabal, X. Bonet-Monroig, A. Dutkiewicz, F. Buda, L. DiCarlo, and L. Visscher. “Calculating energy derivatives for quantum chemistry on a quantum computer.” npj Quantum Inf. 5, 113 (2019). [link]
Written by Youyuan Zhang and Yuya O. Nakagawa.
QunaSys keeps developing efficient quantum algorithms to accelerate various applications of quantum computers. Our mission is to enthusiastically develop technologies that bring out the maximum potential of quantum computers and to continually deliver innovations to society.

 QunaSys Tech Blog
QunaSys Tech Blog