Comprehensive approach for resolving energy spectrum with symmetry using a quantum computer

“Symmetry” appears everywhere in modern physics, and it plays a significant role in understanding various properties of a quantum system. When a quantum system has symmetry, the energy spectrum/states of the system can be classified according to the symmetry; it is known that the symmetry introduces a conserved quantity $C$ (an observable) in a quantum system, and an eigenvalue $c$ of $C$ stipulates a category of symmetry. It is demanding to predict what energies/states appear in each category of symmetry. In quantum chemistry, for example, it is known that light absorption and luminescence only occur among states residing in a certain symmetric category. Thus, to understand photochemical properties of molecules, it is essential to analyze the energies/states of the molecules based on their symmetry.

Meanwhile, a near-term quantum computer called a noisy intermediate-scale quantum (NISQ) device has been recently developed. A NISQ device has been getting attraction as the first step to the realization of more powerful quantum computers. In particular, a NISQ device is expected to simulate a large-sized quantum system that is hard to compute with classical computers. The variational quantum eigensolver (VQE) is a promising algorithm for a NISQ device to compute the ground state and its energy. The VQE utilizes a parametrized quantum circuit $U(θ)$ , an ansatz circuit, to generate a trial state $\ket{ψ(θ)}:=U(θ)\ket{0}$ , an ansatz state. We minimize the expectation value of the Hamiltonian for the ansatz state $\bra{ψ(θ)}H\ket{ψ(θ)}$ as a cost function with respect to the parameters $θ$ to obtain the ground-state energy.

With the growing attention toward a NISQ device, it is suggested to compute energies/states of a given quantum system in the desired category of symmetry by utilizing the modified version of the VQE [1,2], which we call the constrained VQE referring to Ref. [2]. In the constrained VQE, we penalize the deviation of the ansatz state from the desired category to obtain such energies/states with the desired symmetry. More specifically, the following two types of cost functions have been proposed:

F^{(1)}(\theta):=\bra{\psi(\theta)}\hat{H}\ket{\psi(\theta)}+\mu\bra{\psi(\theta)}(\hat{C}-c)^2\ket{\psi(\theta)},\\ F^{(2)}(\theta):=\bra{\psi(\theta)}\hat{H}\ket{\psi(\theta)}+\mu\left(\bra{\psi(\theta)}\hat{C}\ket{\psi(\theta)}-c\right)^2,

where $C$ is a conserved quantity, $c$ is the desired eigenvalue of $C$ , and the coefficient $μ$ , which is called the penalty coefficient, represents the magnitude of the penalty in the cost function. By minimizing those cost functions with respect to $θ$ , we may obtain the optimal parameter $θ^*$ that yields a state $\ket{\psi(\theta^*)}$ belonging to the desired category of symmetry. For example, if we want to compute the energy of the so-called S1 state (the first excited state of singlet) of a hydrogen molecule H2, we consider the electron number operator $N$ , the total spin squared operator $S²$ , and the $z$ -component of spin operator $S_z$ as conserved quantities $C$ and designate the desired category as

N=2, S^2=0, S_z=0.

However, several serious problems prevent practical applications of the constrained VQE. First, the penalty coefficient $μ$ is heuristically chosen without solid theoretical analysis. If the coefficient $μ$ is too small, we may have wrong results; on the other hand, if $μ$ is too large, the optimization may not be completed properly. Currently, there is no guarantee that we can obtain energies/states with the desired symmetry as a result of the VQE. Second, the performance of the two types of penalties has not been compared, leading to the inconsistent use of the two cost functions without any evidence.

In 2020, Kohdai Kuroiwa (an intern at QunaSys Inc.) and Yuya O. Nakagawa (a lead researcher at QunaSys Inc.) provided an extensive analysis of the constrained VQE to solve these problems [3]. They theoretically investigated the two types of penalties in the constrained VQE and disclosed crucial differences between them.

First, for the function $F^{(1)}(\theta)$ , they constructed a simple formula to determine the penalty coefficient with which we can certainly obtain the desired energies/states as a result of the optimization. Conceptually, the formula is constructed by considering the condition that the sum of the expectation energy and the penalty term becomes the smallest for the desired state. Letting $E_\text{ground}$ and $E_\text{target}$ be the ground-state energy and the target-state energy of the Hamiltonian H, respectively, and $C_\text{min}$ be the smallest gap among distinct eigenvalues of $C$ , we have the following formula for the penalty coefficient $μ$ :

\mu\geq \mu^\text{(formula)}:=\frac{E_\text{target}-E_\text{ground}}{C_\text{min}^2}

On the other hand, remarkably, they revealed that $F^{(2)}(\theta)$ does not properly work for any finite value of the penalty coefficients.

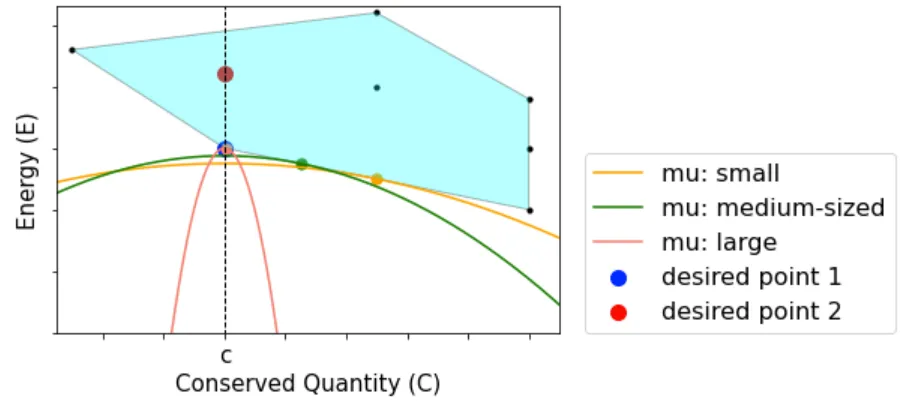
Figure 1

Here, we show the graphical understanding of the reason why $F^{(2)}(\theta)$ does not perform well in Figure 1. In the figure, we hypothetically consider an orthogonal coordinate plane consisting of the expectation values of $H$ and the expectation values of $C$ . A state is mapped to a point on the plane by considering the expectation values of $H$ and $C$ for the state. The black points represent the energy eigenstates of $H$ , and the coordinates of the black points express the eigenvalues of $H$ and $C$ for the eigenstates. The cyan convex polygon corresponds to all the possible points achievable by an ansatz state. The colored curves (yellow, green, and pink) are the contours of $F^{(2)}(\theta)$ with small, medium-sized, and large penalty coefficients μ. In the procedure of the constrained VQE, the point where the curve touches the polygon is regarded as the optimized quantum state. If the desired point (the desired state) is on the boundary of the polygon (the blue point; desired point 1), the optimized point (the tangent point) approaches the desired point but never achieves it in a rigorous sense. On the other hand, if the desired point is in the polygon (the red point; desired point 2), it cannot be the tangent point, and the optimization yields a completely wrong result.

Furthermore, numerical simulations validated these theoretical analyses. The authors of [3] considered a hydrogen chain H4 where four hydrogen atoms are aligned in line with the identical bond distance 2.0 Å. The STO-3G minimal basis set was adopted to construct an 8-qubit Hamiltonian for electronic states. They computed the energy of T1 state (the ground state of triplet) by setting $S² = 2$ and $S_z = -1$ as conserved quantities. They simulated the constrained VQE with the two cost functions having a range of penalty coefficients, $μ = 0.01, 0.1, 1, 10, 100$ . The results are shown in Table 1.

Table 1

In the table, the “residuals” represents the difference between the energy expectation value for the resulting optimized state and that for the desired energy (-1.881 876 Ha) in Hartree (Ha). The result of $F^{(1)}(\theta)$ with $\mu=0.01\simeq \mu^\text{(formula)}$ indicates that the formula leads to the correct value. Note that for large $μ (μ = 10,100)$ , the results of the optimization of $F^{(2)}(\theta)$ is poor for small $μ$ and improves as $μ$ becomes large, which is consistent with the aforementioned graphical explanation. More details and other simulations are shown in the original paper [3].

In conclusion, the analyses of penalties in the constrained VQE revealed the fundamental difference between the performances of the two cost functions $F^{(1)}(\theta)$ and $F^{(2)}(\theta)$ . The inconsistent and heuristic use of the two cost functions will be terminated due to the theoretical superiority of $F^{(1)}(\theta)$ over $F^{(2)}(\theta)$ and the formula to determine the appropriate penalty coefficient. Thanks to the generality of their theoretical analysis, the results have a significant impact on many fields of quantum physics and encourage further investigation for exploiting NISQ devices with the constrained VQE.

References

[1] J. R. McClean et al., “The theory of variational hybrid quantum-classical algorithms”, New Journal of Physics, vol. 18, (2), pp. 023023, 2016.

[2] I. G. Ryabinkin, S. N. Genin and A. F. Izmaylov, “Constrained Variational Quantum Eigensolver: Quantum Computer Search Engine in the Fock Space”, Journal of Chemical Theory and Computation, vol. 15, (1), pp. 249–255, 2019.

[3] K. Kuroiwa and Y. O. Nakagawa, “Penalty methods for variational quantum eigensolver”, Phys. Rev. Research 3 , 013197 (2021)

Written by Kohdai Kuroiwa and Yuya O. Nakagawa.

QunaSys keeps developing efficient quantum algorithms to accelerate various applications of quantum computers. Our mission is to enthusiastically develop technologies that bring out the maximum potential of quantum computers and to continually deliver innovations to society.