Quantum algorithm for calculating electronically excited states of molecules — Subspace-Search Variational Quantum Eigensolver

Quantum chemistry aims to describe the behavior of atoms and molecules. Geometrical structures, molecular vibrational motions, chemical reaction dynamics, and photon absorption and emission are critical characteristics. A complete and accurate electronic structure is a prerequisite for obtaining that information accurately. This requirement brings up the Schrodinger equation, which governs the electrons,

H\ket{\psi}=E\ket{\psi}.

The Hamiltonian $H$ is unique for the target molecule. Solving the Schrodinger equation is equivalent to solving the eigenvalue problem for $H$ , i.e., finding the eigenvectors and the corresponding eigenvalues. However, this problem becomes notoriously hard for classical computers as the size of the molecule increases. It is virtually impossible to precisely solve the Schrodinger equation because the dimension of the Hamiltonian grows exponentially as the number of electrons increases. A complete calculation of a molecule with dozens of atoms will require more classical bits (memories) than the number of atoms in the entire observed universe. However, for quantum computers, the polynomial number of “quantum bits”, or qubits, is required with the increase of the target’s size.

Just like the classical computer takes decades to show its full potential, the quantum computer is coming, but step by step. The first phase is the next three to five years, during which the so-called NISQ (Noisy Intermediate-Scale Quantum) devices are exploited. With various error mitigation methods, NISQ devices are expected to show the quantum advantage at medium size ranging from 50 to a few hundred qubits. Quantum algorithms to solve classically difficult problems with NISQ devices are demanded.

A quantum algorithm for chemistry, called variational quantum eigensolver (VQE) [1], has been developed to solve molecules’ ground states. Usually, molecules stay at their lowest energy states, so the ground state is of particular interest. The VQE utilizes a parameterized quantum circuit $U(\theta)$ , also called an ansatz circuit, to generate an ansatz state $\ket{\psi(\theta)}=U(\theta)\ket{0}$ , where $\ket{0}$ is some reference state. The expectation value of the target Hamiltonian $\braket{H(\theta)}=\bra{\psi(\theta)}H\ket{{\psi(\theta)}}$ is minimized by iterative optimization of the parameters $\theta$ to find the electronic ground state.

Nevertheless, in addition to the electronic ground state, the electronically excited states become essential for studying chemistry. Many attractive phenomena in molecules and materials involve multiple electronic states, such as light absorption and luminescence, nonadiabatic transition, and spectroscopies. This is why a method for computing excited states by NISQ devices is highly desired so that various chemical phenomena can be explored by a quantum computer.

Based on the VQE algorithm for the ground state, there is a naive way to calculation excited states using a quantum computer. Because of the orthogonality between the eigenstates of the Hamiltonian $H$ , to find the $k$ -th excited state is to minimize the expectation value of $H$ under the orthogonal condition, which guarantees that the ansatz $\ket{\psi(\theta)}$ and the ground to $(k-1)$ -th state are orthogonal to each other. In this way, the quantum circuit called “swap test” is necessary for measuring the inner product between the states and checking the orthogonality. However, the swap test brings two significant problems: the required number of qubits becomes twice as large as that of the original system and a lot of SWAP gates are needed, resulting in a deep quantum circuit. In such a case, the overall computational time becomes more prolonged, and the accumulated error will be more significant. So NISQ devices are not considered to be compatible with this method. To obtain excited states using NISQ devices, we need to develop a method without the swap test.

Extending the VQE framework to excited states without the swap test has been achieved recently. In 2018, an intern at QunaSys Inc. Ken Nakanishi, CSO at QunaSys Inc. Kosuke Mitarai, and a professor at Kyoto University (currently Osaka University) Keisuke Fujii proposed an algorithm, the subspace-search variational quantum eigensolver (SSVQE). The general idea is to search a low energy subspace by supplying orthogonal input states to the parameterized quantum circuit $U(θ)$ ; since $U(θ)$ is unitary, the output states become automatically orthogonal and we do not have to check the orthogonality by the costly swap test. The desired $k$ -th excited state can be obtained as the highest energy state in the low energy subspace. The proposed algorithm consists of only the optimization for expectation values of the output states and does not require any ancillary qubits, making this proposal a truly near-term quantum algorithm. Here, we explain one of the variants of the SSVQE, called weighted SSVQE, which gives all the excited states up to the $k$ -th with only one optimization procedure.

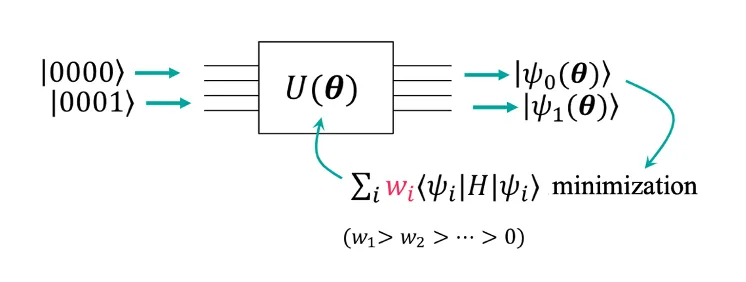
The algorithm of the weighted SSVQE for finding up to the $k$ -th excited state can be described in two steps (see also the figure above):

Construct a parameterized quantum circuit $U(θ)$ and choose input states ${\ket{ψ_j }}_{j=0,1,...,k} =0$ which are orthogonal with each other ( $⟨ψ_i|ψ_j⟩ = δ_{ij}$ ).
Minimize the cost function $L(θ) = Σ_j w_j ⟨ψ_j|U†(θ) H U(θ)|ψ_j⟩$ with respect to $θ$ , where the weight vector $w$ is chosen such that $w_i > w_j$ when $i < j$ .

As we explained, the SSVQE successfully avoids the swap test by using the orthogonal input states. This strategy further benefits us in the evaluation of the transition amplitude between the obtained eigenstates; the transition amplitude $|⟨ψ_i|U^†(θ)AU(θ)|ψ_j⟩|^2$ between two eigenstates for an observable $A$ can be easily evaluated by applying U(θ) to superpositions of the input states like $\frac{1}{\sqrt{2}} (|ψ_i⟩±|ψ_j⟩)$ and measuring expectation values of $A$ . This advantage enables us to investigate the light-matter interaction phenomena involved in quantum chemistry.

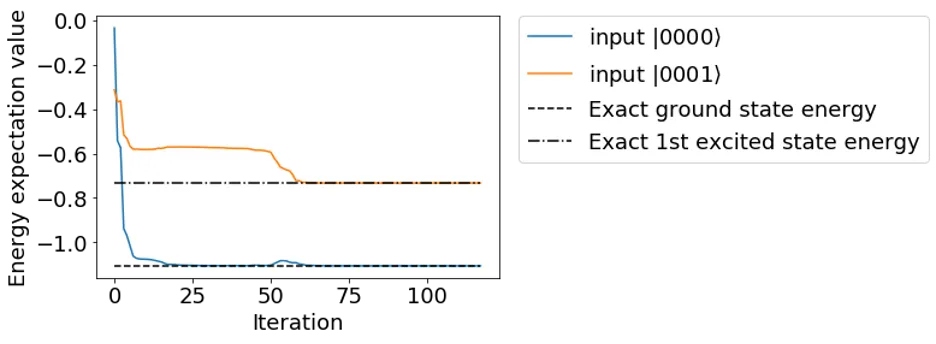
Finally, as a simple demonstration, we implement the SSVQE to search for the ground state and the first (ionic) excited state of a hydrogen molecule. We use the minimal STO-3G basis set to construct a 4-qubit Hamiltonian H to describe the molecule. $|0000⟩$ and $|0001⟩$ are the orthogonal input states fed into the weighted SSVQE algorithm. As you can see in the figure below, the optimization of the SSVQE cost function correctly finds the exact energies of the ground and excited states. The details of the simulation can be found in

[English]

http://docs.qulacs.org/en/latest/apply/6.3_ssvqe.html

[Japanese]

https://dojo.qulacs.org/ja/latest/notebooks/6.3_subspace_search_VQE.html

More examples in details on how to apply SSVQE can be found in the original paper [2].

In conclusion, an efficient algorithm for finding the excited states of a given Hamiltonian is proposed. Unlike the existing algorithms, this method assures the states’ orthogonality at the inputs of the parameterized quantum circuit. Each of the orthogonal input states can be mapped onto one of the energy eigenstates by minimizing a carefully designed cost function by tuning the quantum circuit’s parameters. The whole algorithm is free from the costly swap test and contains only the optimization of the expectation values of several quantum states. Moreover, the transition amplitudes between the obtained eigenstates can be easily evaluated. This new method extends the VQE to excited states without sacrificing any feasibility and will become an important step to take advantage of NISQ devices in practical calculations for quantum chemistry.

Written by Youyuan Zhang, Sho Koh, and Yuya O. Nakagawa

Reference:

[1] A. Peruzzo, J. McClean, P. Shadbolt, M.-H Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’Brien. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5 , 4213 (2014).

[2] Ken M. Nakanishi, Kosuke Mitarai, and Keisuke Fujii. Subspace-search variational quantum eigensolver for excited states. Phys. Rev. Research 1 , 033062 (2019).

QunaSys keeps developing efficient quantum algorithms to accelerate various applications of quantum computers. Our mission is to enthusiastically develop technologies that bring out the maximum potential of quantum computers and to continually deliver innovations to society.