QunaSys Tech Blog

Researchers at QunaSys Inc., Osaka University, and Mitsubishi Chemical Co. have developed an algorithm for calculating the gradient of energy of molecules with a method called state-averaged orbital-optimized variational quantum eigensolver (SA-OO-VQE), which gives a well-balanced description of multiple electronic states and expected to be utilized in a variety of quantum chemistry applications of quantum computers. They have applied the energy derivative calculated based on the developed method to the problem of determining the reaction pathway of cis-trans photoisomerization including a conical intersection, whose analysis requires a balanced description for the ground and excited states, with classical numerical simulation of quantum computers. The results were published in the Journal of Chemical Theory and Computation, a peer-reviewed journal of the American Chemical Society.

“Analytical Energy Gradient for State-Averaged Orbital-Optimized Variational Quantum Eigensolvers and Its Application to a Photochemical Reaction”,

Keita Omiya*, Yuya O. Nakagawa*, Sho Koh, Wataru Mizukami, Qi Gao, and Takao Kobayashi,

Available at: https://doi.org/10.1021/acs.jctc.1c00877

(Preprint version: https://arxiv.org/abs/2107.12705)

In recent years, the development and research of quantum computers have been vigorously pursued. In particular, a type of quantum computer that is now being realized, called a Noisy Intermediate-Scale Quantum (NISQ) device, is expected to outperform existing classical computers in certain tasks [1]. Because NISQ devices are subject to noise, they can only run a few relatively simple algorithms, of which one called the variational quantum eigensolver (VQE) has received the most attention [3]. VQE is a method for calculating the energies of molecules and matter based on quantum mechanics, and it is wisely designed to divide-and-distribute tasks for quantum and classical computers so that it can be easily run on NISQ devices.

In order to make the calculation of molecular energies using VQE more practical, a method called orbital-optimized VQE (OO-VQE) was proposed by several groups including QunaSys [2]. OO-VQE was further extended by combining it with a technique called state-average, and a method called state-averaged OO-VQE (SA-OO-VQE) was proposed [4]. SA-OO-VQE is expected to be applied to various chemical calculations as a method to obtain the ground state (most stable state) and excited state energies of molecules in a balanced manner using a small quantum computer.

Energy is definitely a central quantity that determines the static properties of matter, but it is also very important to know the dynamic properties, for example, how chemical reactions occur. One of the most fundamental quantities for studying dynamic properties is the derivative of energy, that is, how much the energy changes when the parameter of the system is slightly changed. For example, if we know how much the energy changes when the nucleus of a molecule moves slightly, we can find out how the molecule moves afterward.

Although the SA-OO-VQE described above can calculate the energy value itself, there is no known method to obtain its analytical derivative. For NISQ devices, which inevitably contain noise and fluctuation in outputs, calculating the derivative using finite numerical differences is considered to be inaccurate. Therefore, it is vitally important to develop an algorithm to calculate the analytical derivative of the energy.

In this study, we derived a formula for calculating the analytical derivative of the energy in SA-OO-VQE based on the Lagrangian method, which has been used in quantum chemical calculations using classical computers. We showed that the analytical derivative of the energy obtained by SA-OO-VQE can be calculated by appropriately combining quantities that can be easily measured on the NISQ device.

To demonstrate one example usage of this method, we have calculated the SA-OO-VQE energies and their derivatives for a model molecule that exhibits cis-trans photoisomerization including a conical intersection, which is a typical and important photochemical reaction (Fig. 1). The obtained energies and their derivatives were used as a subroutine in an existing method of finding chemical reaction pathways, and it was confirmed that the reaction paths agree well with those obtained by using the SA- CASSCF method, which is the counterpart of SA-OO-VQE on classical computers. This result exemplifies that the calculation of energy and its derivative using SA-OO-VQE can be applied to the analysis of actual photochemical reactions.

The numerical calculations in this study were performed by simulating an ideal quantum computer using a classical computer, and the energies and their derivatives using SA-OO-VQE were calculated by Qamuy, commercial software for quantum chemical calculation by quantum computers developed by QunaSys.

This research has enabled us to calculate a fundamental quantity, the derivative of energy, in a sophisticated method using a quantum computer (SA-OO-VQE). Since the energy derivative is a quantity that is frequently used in computational chemistry, such as in the analysis of chemical reactions, the algorithm developed in this study is expected to further expand the applications of NISQ devices.

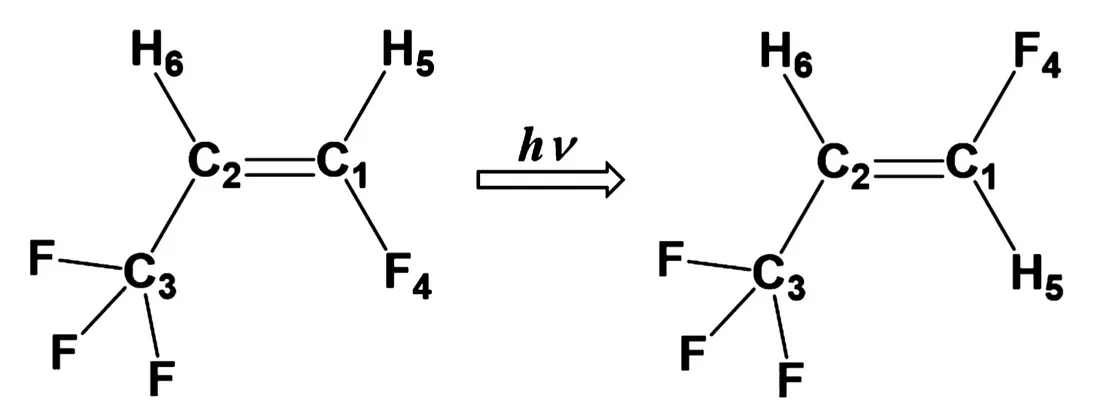
Fig. 1: A model molecule for cis-trans photoisomerization.

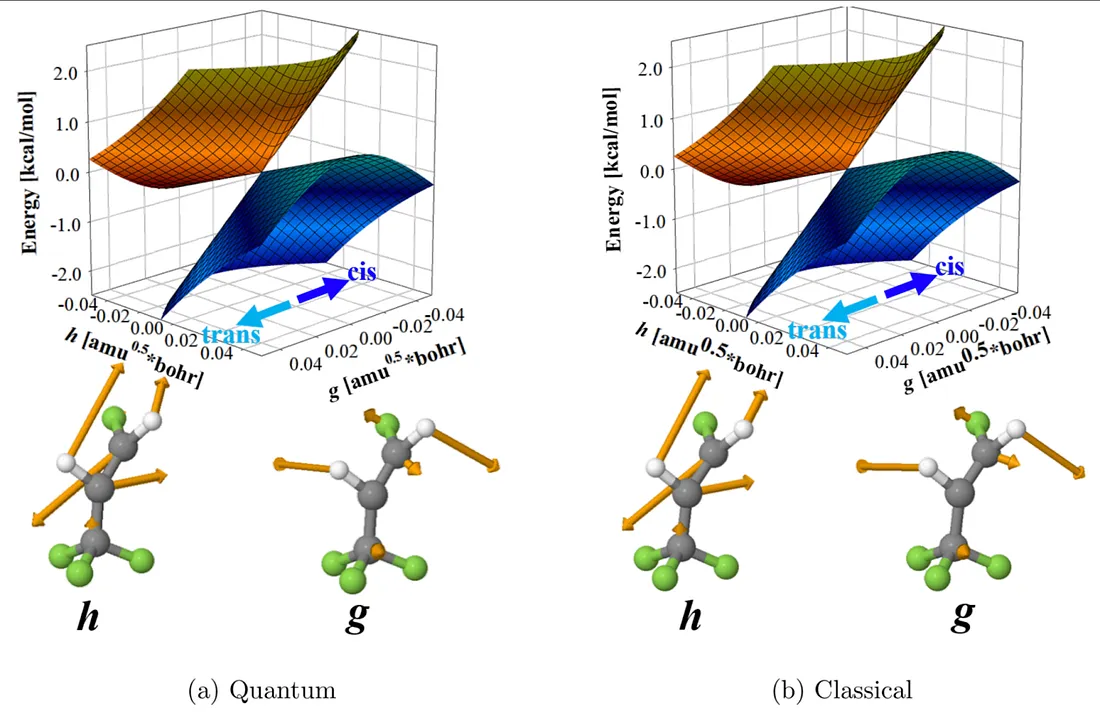
Fig. 2: Potential energy surfaces around the conical intersection between two electronic states involved in the photochemical reaction. Left (right) panel is a result obtained by using SA-OO-VQE (SA-CASSCF).

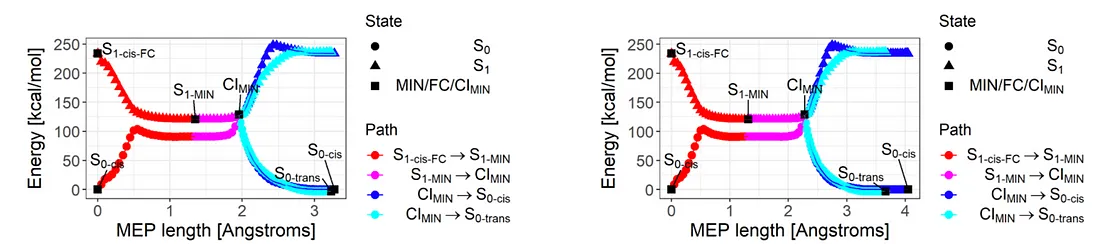
Fig. 3: Plot of energies along the reaction path. Left (right) panel is a result obtained by using SA-OO-VQE (SA-CASSCF).

[1] F. Arute et al., Nature 574, 505–510 (2019), https://www.nature.com/articles/s41586-019-1666-5

[2] A. Peruzzo et al., Nat. Commun. 5, 4213 (2014) https://www.nature.com/articles/ncomms5213

[3] T. Takeshita et al., Phys. Rev. X 10, 011004 (2020)

https://journals.aps.org/prx/abstract/10.1103/PhysRevX.10.011004,

I. O. Sokolov et al., J. Chem. Phys. 152, 124107 (2020), https://aip.scitation.org/doi/10.1063/1.5141835,

W. Mizukami et al., Phys. Rev. Research 2, 033421 (2020),

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.033421,

[4] S. Yalouz et al., Quantum Sci. Technol. 6 024004 (2021), https://iopscience.iop.org/article/10.1088/2058-9565/abd334