Computational Fluid Dynamics (CFD) calculations are a promising application for quantum computers. In this tech blog article, we report on the results of research conducted by an in-house team of QunaSys intern Ueno and QunaSys researchers. In this project, we developed the essential technology for practical application in response to prior research, and implemented and simulated quantum circuits using QunaSys' QURI SDK.
CFD Calculations and Quantum Computers
In CFD calculations, as in other computer-aided engineering (CAE) calculations such as electromagnetic field analysis and structural analysis, space is divided into a mesh and values are maintained for flow velocity and pressure at each point. In simulation calculations, fluid flow is simulated by updating the values at each point in successive time steps. In many cases, the number of meshes required increases significantly, especially when the difference in scale between the vortex of the object and the fluid is large, such as in passenger aircraft, and this is handled by reducing the number of meshes by using approximate models of turbulence.
On the other hand, quantum computation is expected to have the potential to handle meshes with an exponentially large number of grid points. A quantum computer can hold N numbers using only log(N) qubits, for example, 40 qubits can hold 1 trillion numbers. Although recent research [1] has pointed out that there may not be a strong quantum advantage in CFD calculations in terms of computation time, called "exponential speedup," the practical advantage is still strongly expected.
In the rest of this article, we will discuss the implementation of quantum circuits using a technique called the lattice Boltzmann method. First, we will explain the lattice Boltzmann method, followed by an introduction to previous research on its use in quantum computer calculations, and finally, we will present our research results.
Lattice Boltzmann Method
CFD calculations are usually performed by solving differential equations called the Navier-Stokes equations. The Navier-Stokes equations describe the motion of fluids such as air and water. The Navier-Stokes equations are based on the basic variables of flow velocity and pressure at each point in space, and can be said to describe fluids on a macroscopic scale (much larger than molecules).
However, a more microscopic formulation is also possible, since air and water are actually collections of molecules, and molecules move according to Newtonian mechanics (or more precisely, quantum mechanics). The lattice Boltzmann method is a method that utilizes this approach, but on a macroscopic scale, similar to the Navier-Stokes equations. The starting point for the lattice Boltzmann method is the Boltzmann equation, which describes the motion of a collection of molecules. The Boltzmann equation describes the motion of a fluid by taking as variables the distribution functions for the velocity and position of the molecules and describing their collisions and movements. Although the Boltzmann equation is a more microscopic description than the Navier-Stokes equation, it is known that under certain conditions they are equivalent.
In the lattice Boltzmann method, the Boltzmann equation is applied to a space discretized by a grid and the distribution function is calculated at each grid point. Because it involves several approximations in the formulation process, the method is mainly applied to simulations of fluids called weak compressible fluids, but it has attracted attention again in recent years due to the advantages such as its high parallelism.
In quantum computation, the lattice Boltzmann method is expected to be more efficient than the direct solution of the Navier-Stokes equations, as it can be implemented as a fixed quantum circuit for operations at each time step independent of the state. Research on lattice Boltzmann's method of quantum computer computation began around 2021 [2], and theoretical algorithms were proposed in Ref. [3]. In Ref. [4], a more concrete implementation of the algorithm of Ref. [3] was studied and the number of qubits and quantum gates were estimated. Note that the estimates in Ref. [4] may contain some errors, such as overestimating the number of qubits, and care should be taken in interpreting the numbers.
Prior Studies and Issues
The workflow in Ref. [4] is based on a linearized lattice Boltzmann method calculation that incorporates nonlinear effects in a technique known as Carleman linearization, using the simulation of flow around a sphere as the problem setting. Specifically, the quantum computation is accomplished by executing a quantum circuit with the following nested structure of subroutines
- Quantum amplitude estimation to compute the drag force
- Subroutine to produce the final-state calculation, called multiple times within the quantum amplitude estimation
- Subroutine to perform a single time step calculation, called multiple times within the end-state calculation
However, Ref. [4] does not actually implement and simulate quantum circuits, but only makes specific estimates of the number of qubits and quantum gates. The estimates of the number of qubits and gates included approximations and upper bounds, and also left open issues such as the quantitative handling of nonlinear effects and the implementation of inflow and outflow boundary conditions.
In the next section, we present our research addressing these issues.
QunaSys' work
Linearization
First, we performed an analysis of the Taylor-Green vortex as a case study of incorporating nonlinear effects through linearization, and found that the relative error is roughly proportional to the simulation time.
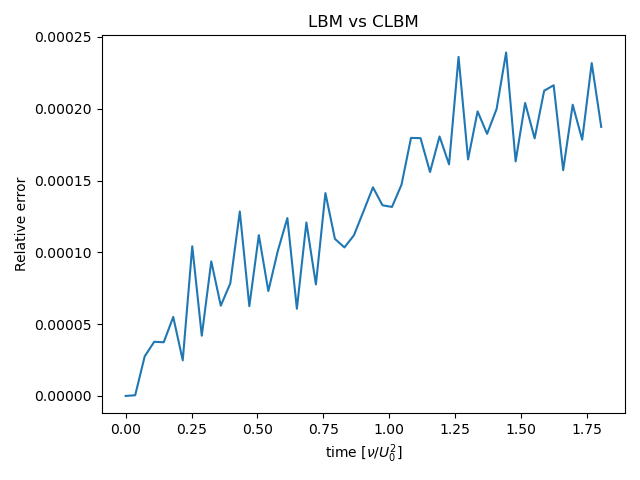
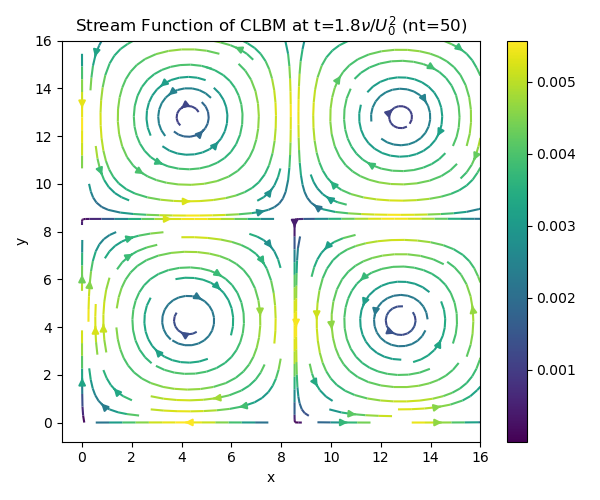
Computational cost
Before starting specific implementation, we performed a numerical analysis to confirm the computational complexity. One particularly important value is the "condition number," which increases the computational complexity if the condition number is large. We examined how the condition number scales with grid size in fluid simulations. As a result, we found that the larger the Reynolds number, the smaller the change in the condition number with grid size. This is a promising result considering that the larger the Reynolds number, the more difficult it is to simulate and the greater the importance of quantum computation.
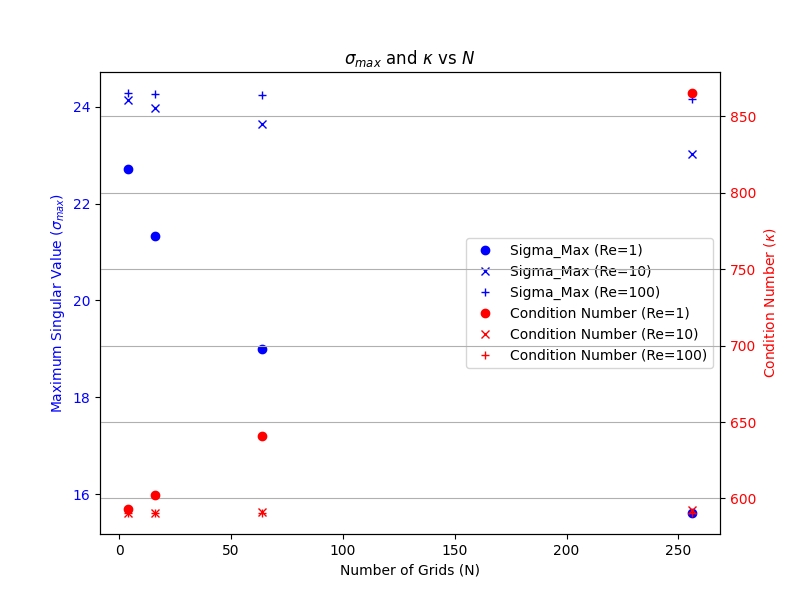
Boundary Conditions
The treatment of boundary conditions around objects has already been treated in Ref. [4], but boundary conditions for inflow and outflow are also necessary for fluid simulations. In this project, we have also studied this issue and have made it possible to implement quantum circuits.
Quantum Circuit Implementation and Simulation
Finally, we will implement quantum circuits and perform quantum circuit simulations (on a normal computer). We chose a fluid simulation in which a plate-like object is placed in a two-dimensional space with a 16 x 32 = 512 grid, and we used an approximation that ignores the second-order or higher contribution of the Carleman linearization, i.e., nonlinear effects are ignored.
The QURI SDK developed by QunaSys was used for the implementation. qsub interface of QURI Parts, which is part of the QURI SDK, makes it possible to implement complex quantum circuits in FTQC algorithms like ours in a structured manner using subroutines. For more information on qsub, please refer to the qsub tutorial.
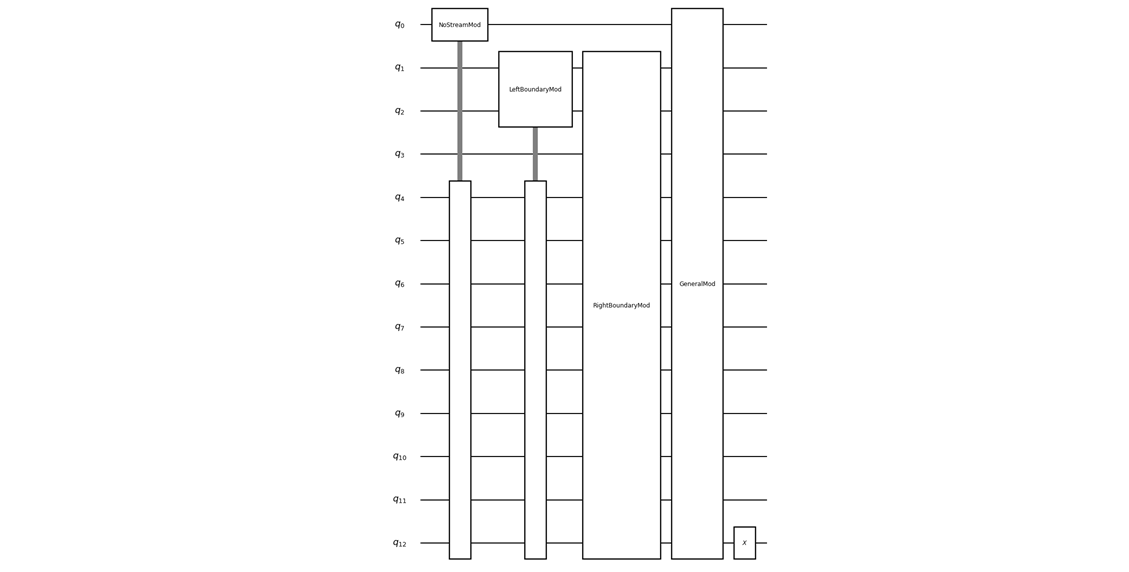
For the simulation, we used the quantum circuit simulation library Qulacs through the QURI SDK.
In this project, we implemented a quantum circuit for one time step and repeated the time evolution. The results are as follows (classical: computed by the usual lattice Boltzmann method, quantum: computed by quantum circuit simulation), demonstrating that quantum circuit simulation can indeed simulate fluid flow as expected.

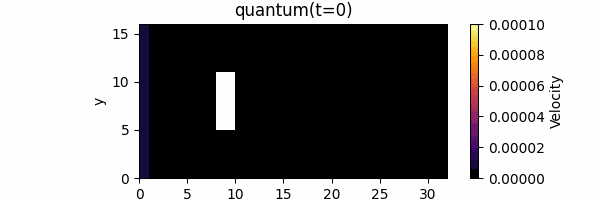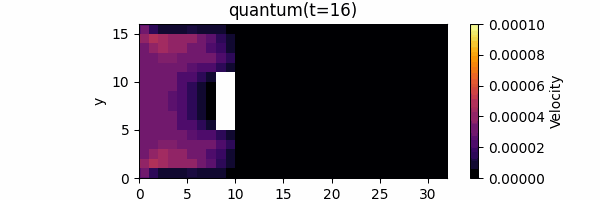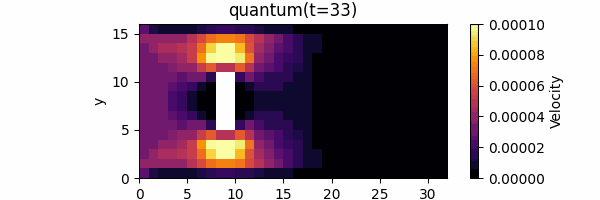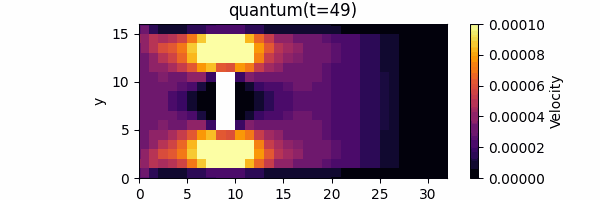
Summary and Prospects
Fluid simulation has long been considered a promising application of quantum computation, but there have been few examples of scalable quantum circuit implementations and demonstrations. In this project, we have successfully demonstrated fluid simulation using quantum circuits by extending the proposals in Refs [3], [4].
As the future work, we will continue our research and development to realize fluid simulation by quantum computation, including consideration of nonlinear effects, simulation of more complex problems, and simulation including calculation of physical quantities such as drug force.
References
[1] K. Sakamoto and K. Fujii, "On the quantum computational complexity of classical linear dynamics with geometrically local interactions: Dequantization and universality. Dequantization and universality," arXiv:2505.10445 [quant-ph] (2025).
[2] L. Budinski, "Quantum algorithm for the Navier Stokes equations by using the streamfunction vorticity formulation and the lattice Boltzmann method ", International Journal of Quantum Information 20(2) 2150039 (2022)
[3] X. Li, X. Yin, et al, "Potential quantum advantage for simulation of fluid dynamics", Phys. Rev. Res. 7, 013036 (2025)
[4] J. Penuel, A. Katabarwa, et al., "Feasibility of accelerating incompressible computational fluid dynamics simulations with fault- tolerant quantum computers", arXiv:2406.06323 [quant-ph] (2024)

 QunaSys Tech Blog
QunaSys Tech Blog