QunaSys Tech Blog

For some problems in physical science, we need to take care of quantum information to compute or simulate target physics because it is described by quantum mechanics. In most cases, however, it is hard to handle such quantum information on classical computers. Given that, it is natural to think of processing quantum information as it is by a quantum computer, like Feynman’s famous quote, “Nature isn’t classical, dammit, and if you want to make a simulation of nature, you’d better make it quantum mechanical”[1]. Today, we are witnessing the realization of prototypical digital quantum computers; quantum devices consisting of hundreds to thousands of non-fault tolerant qubits (quantum bits), the so-called noisy intermediate-scale quantum (NISQ) devices, have been developed rapidly in the past few years. Some commercial companies start providing access to their early-stage NISQ devices to their customers, although the devices seem still too small and noisy to execute any industrially-competitive tasks.

Meanwhile, the rapid growth of machine learning algorithms has been applied to various fields in physical science, allowing us to solve problems that have no analytical solution and require a huge amount of computational resources even with numerical methods. So, even though the allowed computations on the NISQ devices are quite limited, combining machine learning algorithms with the quantum devices may circumvent such computational burdens for solving quantum problems, and they may accelerate the applications of the NISQ devices to reach the industrial level.

Quantum chemistry, which studies properties of chemical materials based on quantum mechanics, is one of those fields with wide applications of machine learning. The main task of quantum chemistry is to solve the Schrödinger equation, a fundamental equation of quantum mechanics, to predict various chemical phenomena such as chemical reactions. Although many computational methods for solving the equation on classical computers have been developed for decades, they often require gigantic computational resources, which prevent us from investigating many interesting and industrially-important processes such as photo-excitation dynamics of molecules.

One of the promising ways to make use of the NISQ devices for quantum chemistry is the so-called variational quantum eigensolver (VQE), which is a variational algorithm finding the ground state (the most stable state) of a given quantum system [2]. The key idea of the VQE is to combine a programmable and parametrized quantum circuit implemented on the NISQ devices with a classical optimization technique. By optimizing the quantum circuit classically, the VQE algorithm can find the ground state of the system with only a shallow quantum circuit that is presumably executable even on the NISQ devices.

The ground state does not describe the whole physics of the quantum system, but the excited states are also essential to analyze it. Nonetheless, even though extensions of the VQE to find excited states have been proposed recently by several researchers [3], they usually require a larger number of runs of the quantum circuit than the VQE does, and therefore it is not so easy to run them on the real NISQ devices.

To present another approach to find the excited states of quantum systems, Hiroki Kawai (a former intern at QunaSys Inc.) and Yuya O. Nakagawa (a lead researcher at QunaSys Inc.) proposed a simple quantum machine learning scheme, or a machine learning algorithm utilizing a quantum computer [4]. Their proposal aims to learn physical quantities from quantum data. Its capability was demonstrated to predict the properties of electronic excited states of small molecules. The model is trained with supervised machine learning from only its ground state wavefunction realized as a qubit state on the NISQ devices. It has the following distinct features:

• It learns wavefunctions of the target system that are "quantum" data. Most quantum machine learning algorithms treat classical data such as text, images, etc., and have the difficulty of encoding classical data in quantum states on quantum computers. Learning from quantum data is a natural setup of performing quantum machine learning, and there is no overhead in encoding the data into quantum states because the data are already quantum.
• Quantum information should give a more accurate description of the molecular system than classical information, which is so far used for classical machine learning methods applied to quantum chemistry.
• It reduces the cost of finding the excited states because it only requires the quantum data of the ground state obtained by the usual VQE whose resource requirements are less than finding the excited states by the extensions of the VQE.
• It may be executable on the NISQ devices since the required circuit depth is shallow.

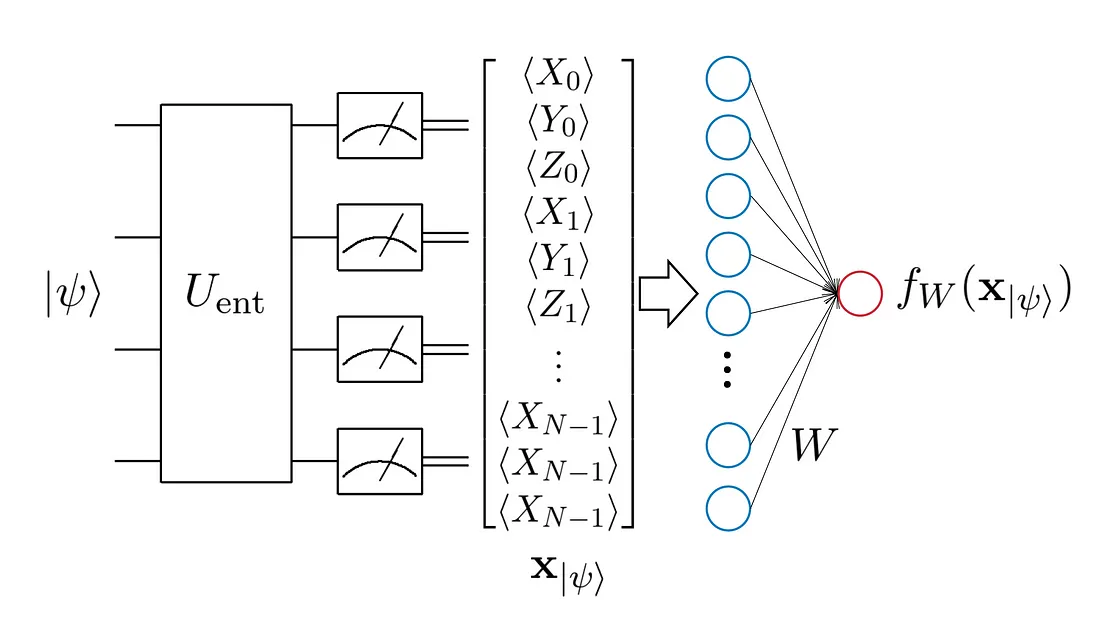
Figure 1. Schematic diagram of our model. $\ket{\psi}$ is the input state (the ground state of a molecular Hamiltonian in our setup). $U_\text{ent}$ is the quantum reservoir. The gauges indicate single-qubit measurements from which one obtains the classical vector $\mathbf{x}$ and the vector is fed into the machine learning unit $f$ with weights $W$.

Let us describe the details of the algorithm. As well as the VQE, it has both the quantum and classical parts (Fig. 1). First, we input a quantum state that is the ground state of the target Hamiltonian, which is computed by the VQE beforehand. The quantum part consists of a random quantum circuit called quantum reservoir (specified as $U_\text{ent}$ in Fig. 1) and the single-qubit Pauli measurements. The reservoir, which can be any kind of random quantum circuit and is fixed during the learning, increases the entanglement of the input quantum state so that one can obtain non-local information from only the measurements of the local, single-qubit Pauli operators (we note that quantum reservoir was introduced in [5]). The measurements in the quantum part of the algorithm give a $3N$-dimensional classical real-valued vector

where $N$ is the number of qubits. Conducting only the single-qubit Pauli measurements makes it easy to implement the algorithm on the near-term NISQ devices. Moreover, as few as three different circuits are needed to obtain the vector $\mathbf{x}$ since the single-qubit operators acting on different qubits commute with each other, and hence the measurements of them can be performed simultaneously. After obtaining the classical vector, the algorithm proceeds to the classical part which is a simple classical machine learning unit, e.g. linear regression. The classical machine learning unit is trained to predict the excited-state properties of the target Hamiltonian from this vector $\mathbf{x}$. More details can be found in the original paper [4].

In [4], numerical simulations for small molecules (LiH and H_4) with various geometric structures were performed to demonstrate the applicability of the method to problems in quantum chemistry.

The Hamiltonians for electronic states of the two molecules are considered. The first and second excited energies of the Hamiltonian and the transition dipole moment from the ground state to the first excited state are chosen as the target excited-state properties that the proposed algorithm seeks to predict from the ground state wavefunctions. The authors numerically simulated two situations; one is the noiseless situation, where the ideal outputs from the quantum circuits are available, and the other is the noisy situation, where the quantum circuit has noise and the measurement results have statistical and systematic errors.

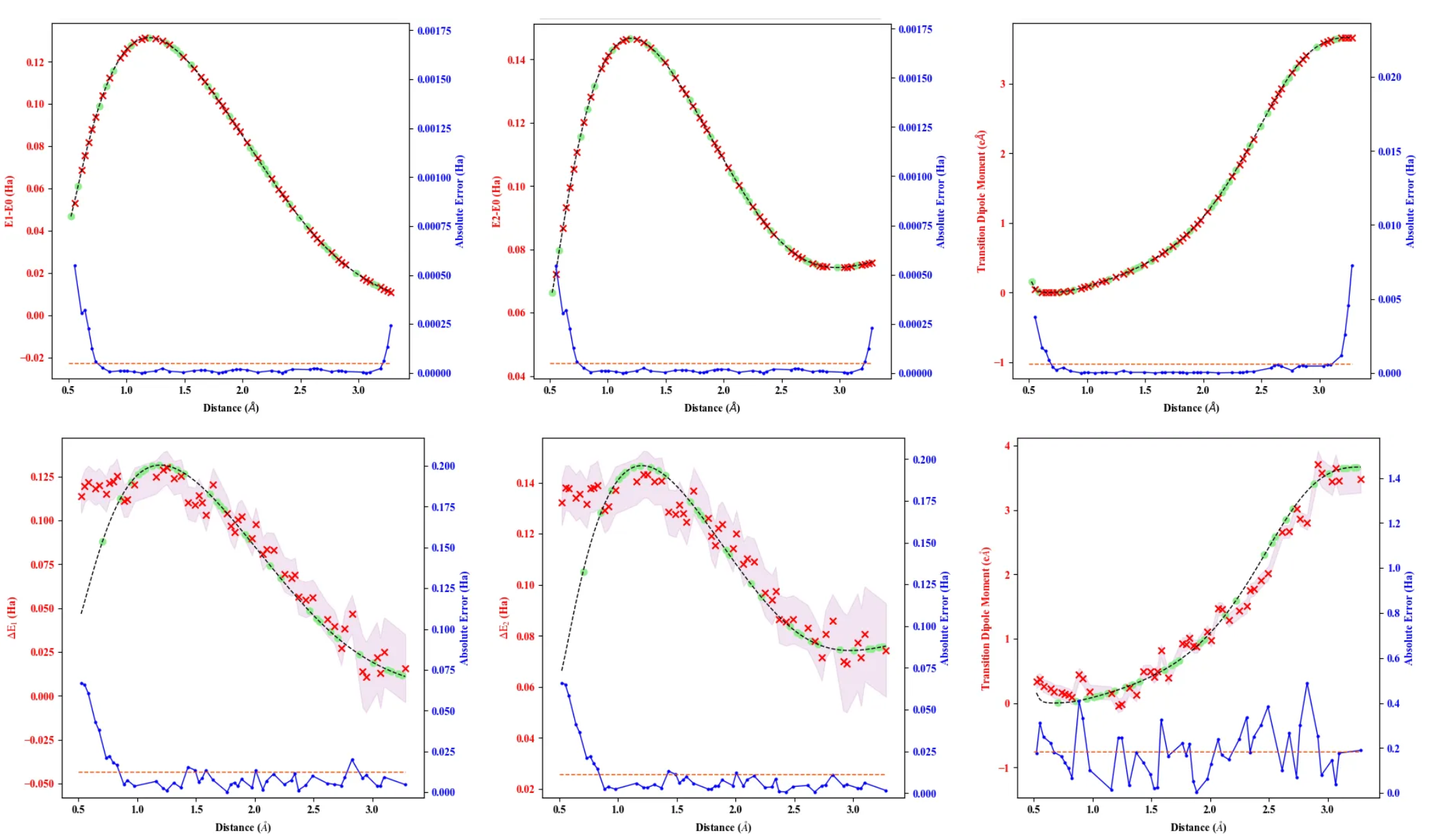
Figure 2. The prediction results by the trained model for LiH with various bond lengths for the noiseless simulations (top row) and the noisy simulations (bottom row). The left, center, right columns present the results for the 1st excitation energy, the 2nd excitation energy, and the transition dipole moment, respectively. AE represents the absolute error between the predictions and the exact values, and MAE does the mean of AE.

The prediction results for the LiH molecule as an example are shown in Fig. 2. We can see that the proposed algorithm predicts the exact values of the excited-state properties with high precision for the noiseless cases. Even in noisy cases resembling the actual NISQ devices, it reproduces the approximative values.

In conclusion, Kawai and Nakagawa introduced a new quantum machine learning scheme for predicting the excited-state properties of a molecular Hamiltonian from its ground state wavefunction. It consists of a random quantum circuit called a quantum reservoir and a simple classical machine learning unit. The numerical simulations demonstrated that it can accurately predict the target excited-state properties and has the potential to be implemented on a near-term NISQ device. Although numerical demonstrations were performed only for the small molecules, we expect that it is applicable to larger molecules appearing in more practical applications in quantum chemistry and material science in the future.

[1] Feynman R P, International Journal of Theoretical Physics 21 467–488 (1982)

[2] Peruzzo A, McClean J, Shadbolt P, Yung M H, Zhou X Q, Love P J, Aspuru-Guzik A and O’Brien J L, Nature Communications 5 4213 (2014)

[3]

McClean J R, Kimchi-Schwartz M E, Carter J and de Jong W A, Phys. Rev. A 95, 042308 (2017),

Colless J I, Ramasesh V V, Dahlen D, Blok M S, Kimchi-Schwartz M E, McClean J R, Carter J, de Jong W A and Siddiqi I, Phys. Rev. X 8, 011021 (2018),

Nakanishi K M, Mitarai K and Fujii K, Phys. Rev. Research 1, 033062 (2019), see also this blog post,

Parrish R M, Hohenstein E G, McMahon P L and Martınez T J, Phys. Rev. Lett. 122, 230401 (2019),

Higgott O, Wang D and Brierley S, Quantum 3 156 (2019),

Jones T, Endo S, McArdle S, Yuan X and Benjamin S C, Phys. Rev. A 99 062304 (2019),

Ollitrault P J, Kandala A, Chen C F, Barkoutsos P K, Mezzacapo A, Pistoia M, Sheldon S,Woerner S, Gambetta J and Tavernelli I, Phys. Rev. Research 2, 043140 (2020),

Tilly J, Jones G, Chen H, Wossnig L and Grant E, Phys. Rev. A 102, 062425 (2020)

[4] Kawai H and Nakagawa Y O, Mach. Learn.: Sci. Technol. 1, 045027 (2020)[5] Fujii K and Nakajima K, Phys. Rev. Applied 8, 024030 (2017)

Written by Hiroki Kawai and Yuya O. Nakagawa.

QunaSys keeps developing efficient quantum algorithms to accelerate various applications of quantum computers. Our mission is to enthusiastically develop technologies that bring out the maximum potential of quantum computers and to continually deliver innovations to society.