QSCI法を用いた分子基底エネルギーの実機量子計算の実証

こんにちは、リサーチチームの池田です。

去る2023年12月4日〜6日、ニューヨークで行われたIBM Quantum Summit 2023にて株式会社ENEOS様と我々の共同研究の成果を発表いたしました。本記事ではその共同研究内容についてご紹介します。

量子化学計算は系そのものが持つ量子性から、量子コンピュータの有力な応用先の一つとして期待されています[1]。従来の量子計算ではNISQ(Noisy Intermidiate Scale Quantum)デバイスを用いた変分量子計算が盛んに行われていますが、必要な統計エラー内に抑えるために沢山のショット数とステップ数が必要である点、統計誤差のために現在の実機計算結果はvariationalでない点、現在の実機の性能ではノイズの影響が非常に大きい点が課題として知られています。

我々が提案したQSCI(Quantum Selected Configuration Interaction)法[2]は実機量子コンピュータの用途を量子サンプリングに限定することで、より高精度のエネルギー計算を可能としています。

QSCI法のアルゴリズムは以下のようになっています：

量子コンピュータの入力状態 $\ket{\psi_\mathrm{in}}$ を準備する
これはVQE(Variational Quantum Eigensolver)等で適度に最適化された入力状態を指しています。
入力状態を用いて実機量子測定を行う
入力状態を計算基底で繰り返し量子測定します。
重要な電子状態を選択する
測定されたビット列から頻度の高いものを順に ~~$R$~~ 個適当な数だけ選択する
選択したビット列を用いて有効ハミルトニアンを構成し、それらを厳密対角化する
得られた結果 $E$ は厳密解 $E_{\mathrm{exact}}$ に対して、 $E \ge E_{\mathrm{exact}}$ であることがノイズのある実機でも保証されます。

今回我々はQSCI法を２つの分子ハミルトニアン（ジアゼン $\text{H}_2\text{N}_2$ 、メタン $\text{CH}_4$ )について適用し、得られた成果をIBM Quantum Summit 2023にて報告いたしました。量子サンプリングに実機量子コンピュータ（ibm_algiers）を用いたことを強調したいと思います。

ジアゼン( $\text{H}_2\text{N}_2$ )

まずQSCI法の入力状態としてどういったものが適してるのかを調べるため、ジアゼン分子におけるVQE計算のエネルギー精度をシミュレーターにおいてさまざまなansatzについて調べました。標準的なRy ansatzではHartree-Fock (HF)と同程度のエネルギー精度で収束したのに対し、後述するRy Custom 1 ansatz (以下Ry Custom ansatz)ではCASCI(4e,4o)で得られたエネルギーと同程度のエネルギー精度を得ることができました。

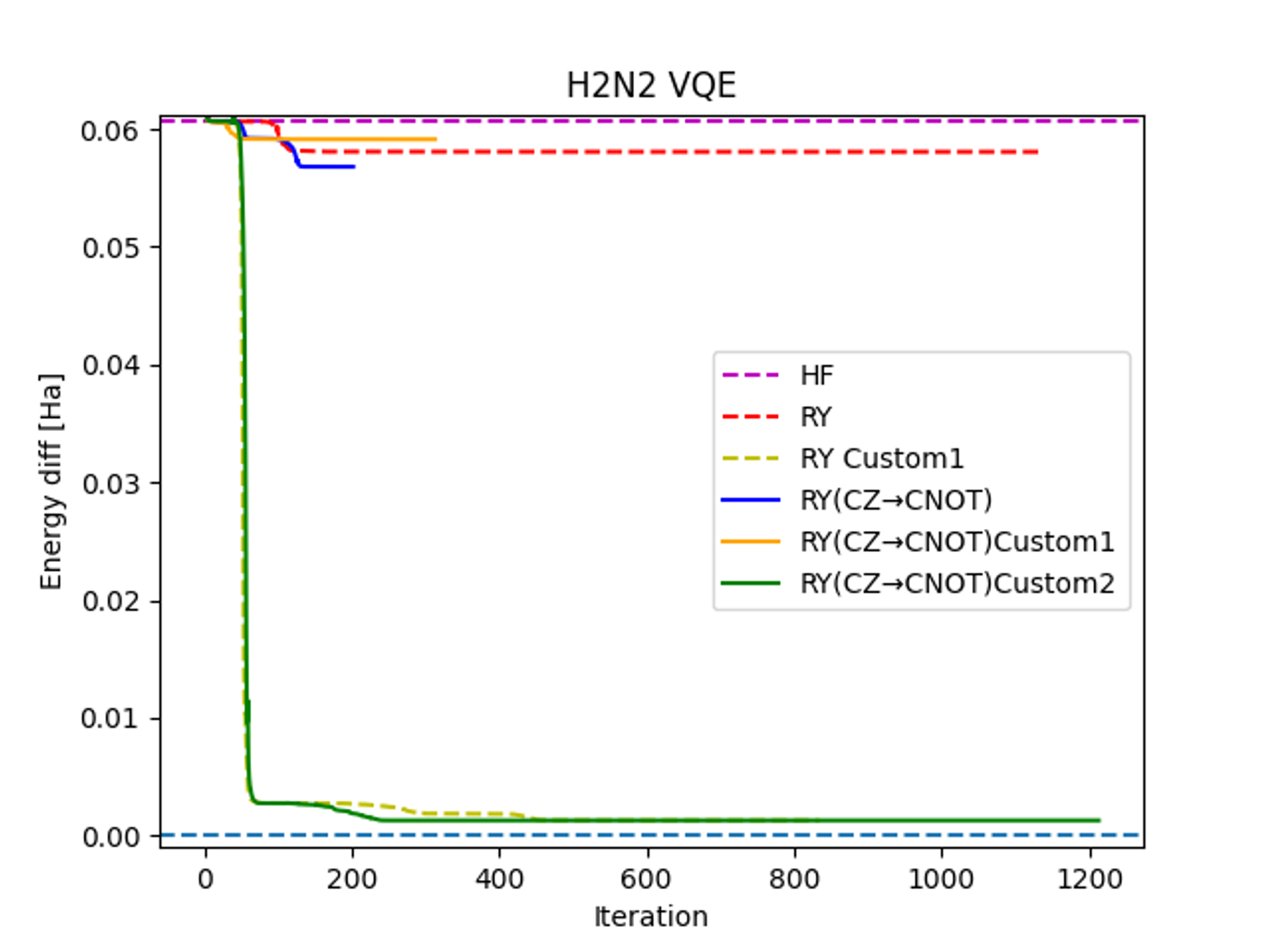
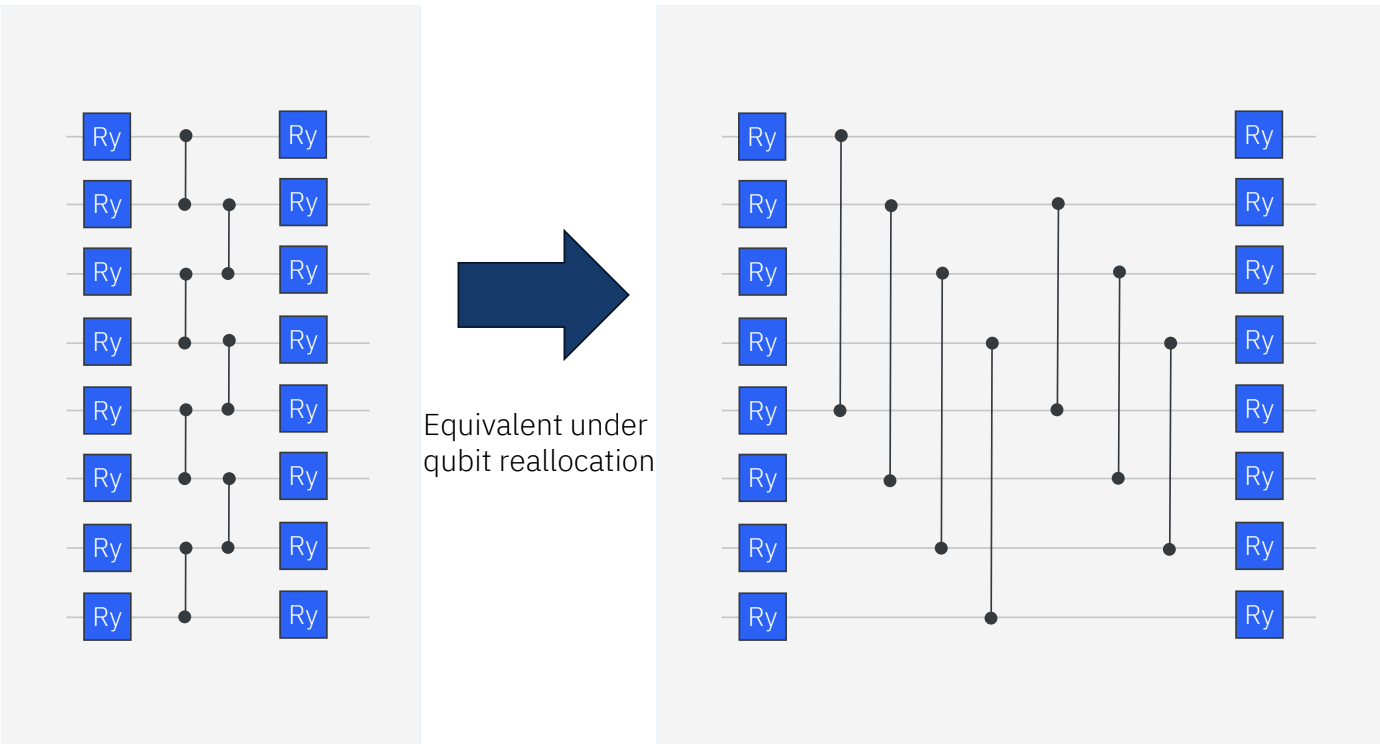
Ry Custom ansatzは次の図2.のようにCZ gateのかけ方を変更したものになっています。この配置は標準的なRy ansatzからqubitを再配置することで得られるものです。物理的な意味合いとしては、占有軌道と仮想軌道とをエンタングルさせていることに相当します。今回の結果は、回路のトポロジーだけでなく、エンタングルペアの選択が結果に大きく影響することを示唆しています。

こうしてシミュレーターで得られたVQE入力状態を実機コンピュータに入力することで実機QSCIを行いました。この系は8-qubit系であり、実機としてはibm_algiersを用いました。計算結果は表1の通りになります。

表1.各計算手法におけるジアゼン分子ハミルトニアンの基底エネルギー(単位はHartree)。HF: Hartree-Fock計算によるエネルギー。Input VQE: 深さ8のRy Custom ansatzを用いて最適化された状態のエネルギー。Demonstrated QSCI: 上記状態を入力とするQSCIを実行して得られたエネルギー。shot数は10000回とし、測定されたすべての状態を用いて有効ハミルトニアンを構成した。CASCI(4e,4o): 活性空間の範囲内で厳密対角化して得られたエネルギー。

Method	Energy [Ha]
HF	-108.5570
Input VQE	-108.6163
Demonstrated QSCI	-108.6176
CASCI(4e,4o)	-108.6176

実機を用いたQSCIのの計算精度がシミュレーターVQEのそれを上回り、さらに厳密な計算であるCASCIと高い精度で一致することがわかりました。

またQSCIの入力状態として最適化具合の異なるシミュレータVQEの計算結果を用いて、実機QSCIの計算性能を検証しました(図3)。

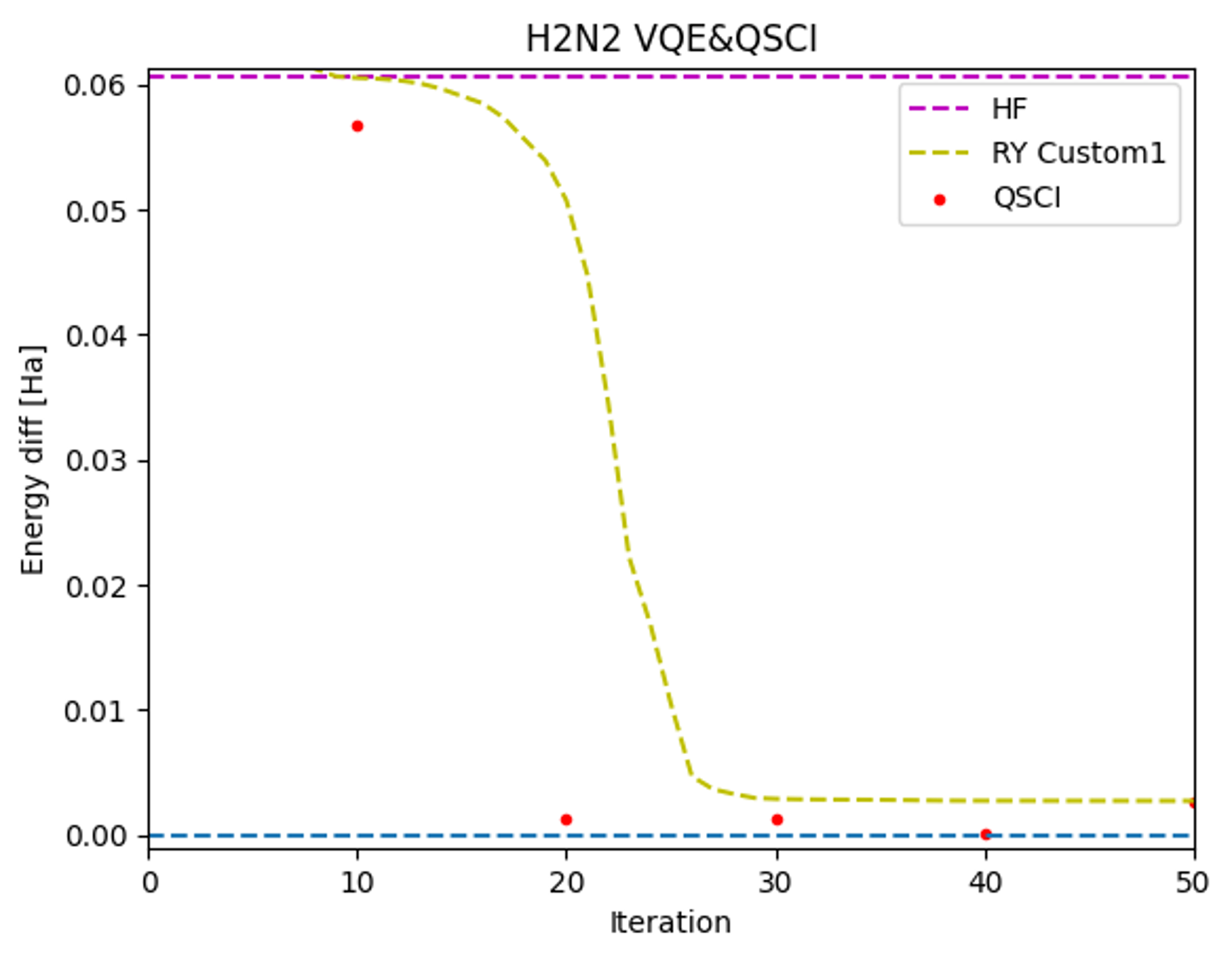
実機QSCIはいずれもシミュレータVQEで得られた計算よりも高精度の計算結果を示しました。特に反復数が20程度のVQE入力状態においても実機QSCIで高精度の基底エネルギー計算ができました。このように最適化が不完全な状態であってもQSCIにより精度良くエネルギーが計算できたことから、最適化に長い時間がかかるというVQEの課題の一つが克服できる可能性があります。

メタン( $\text{CH}_4$ )

次により大きな分子系としてメタン( $\text{CH}_4$ ,16-qubit系)を例に取り、水素原子の解離反応

\text{CH}_4 → \text{CH}_3 + \text{H}

について同様に実機QSCIを行いました。計算においては、水素原子と炭素原子の結合長を変化させることで現象を再現しています（最安定結合長は1.083[Å]）。

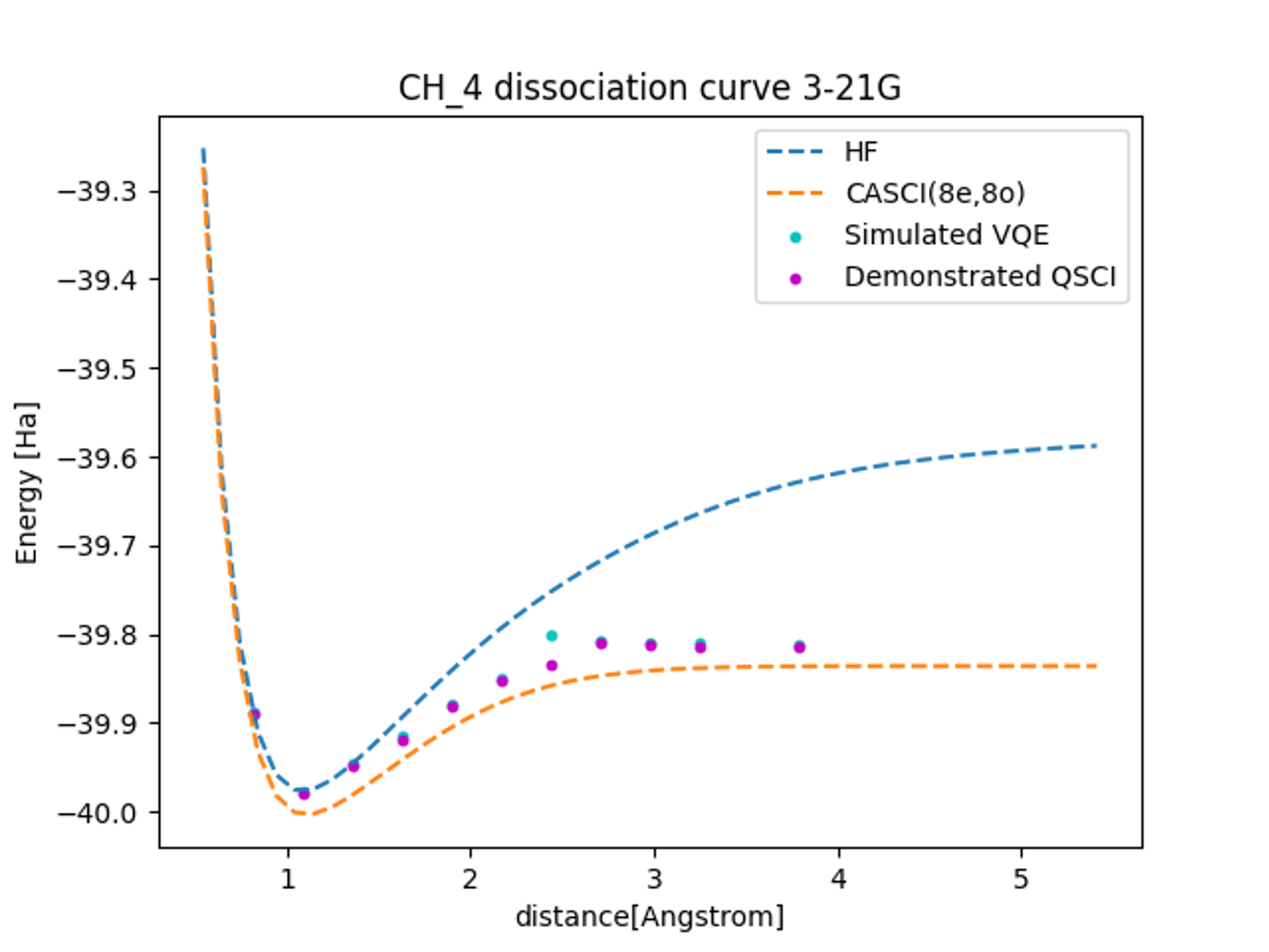
計算の結果、各計算手法における基底エネルギーの解離曲線は図4のようになりました。結合長が伸びるにつれハートリー・フォック計算と厳密解の差が大きくなることからもわかるように、解離反応では電子相関の寄与が重要になります。

16-qubit系における実機QSCI計算結果はノイズのないシミュレーターVQEの計算結果と比較しても（特に中間領域において）精度の良い結果が得られていることがわかります。今回はシミュレーションのみで実機におけるVQE計算は行いませんでしたが、仮に今回のQSCI計算と同じく10000ショットの実機計算を行ったとすると、0.1[Ha]程度の統計誤差があると考えられます。今回の結果によって16-qubitと従来の実機を用いた量子化学計算と比較して大きな系においても、QSCI法を用いることでVQEよりも高精度の結果が得られることが分かりました。

結論

今回我々は二つの化学分子（ジアゼン $\text{H}_2\text{N}_2$ ,メタン $\text{CH}_4$ ）の基底エネルギーを、量子コンピュータ(ibm_algiers)による実機量子計算で求めました。計算では我々が開発したQSCI法を用いました。

ジアゼン分子（8-qubit）の実証では：

実機を用いたQSCI法による計算結果はCASCI(4e,4o)による厳密解を高い精度で再現しました。
入力状態の最適化度合いに対してQSCI法はロバストであることが実機計算において実証されました。

またメタン分子（16-qubit）の解離反応における実証では：

QSCI法を用いた実機量子計算はシミュレータを用いたVQE計算結果より高い精度の結果が得られました。

参考文献

[1] S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin, and X. Yuan,
Reviews of Modern Physics 92, 015003 (2020).

[2] K. Kanno, M. Kohda, R. Imai, S. Koh, K. Mitarai, W. Mizukami, and Y. O. Nakagawa, arXiv: 2302.11320 (2023).

執筆者：池田侑平、筒井翔一朗、菅野恵太