こんにちは、ソフトウェアエンジニアインターンの柚木隼人です。
近年様々なアルゴリズムが開発され注目を集めたNoisy Intermediate Scale Quantum (NISQ) から、長期的に目指されているFault Tolerant Quantum Computing (FTQC) への中間的な存在として、Early-FTQCと呼ばれるデバイス向けのアルゴリズムが盛んに研究されています。Early-FTQCには以下のような特徴があります。
- 量子ビット数やゲート数に制限があるためこれらを節約するアルゴリズムが必要
- 誤り訂正が部分的 (例えばCliffordゲートだけ誤り訂正)
- 誤り訂正の符号長が短い、かつ魔法状態蒸留が不十分
2022年にEarly-FTQC向けのアルゴリズムとして、Heisenberg limitを達成しながら基底状態のエネルギーを推定する手法が提案されました[1]。本記事ではこの論文を解説し、提案された手法をQURI Parts[2]を用いて実装する方法を紹介します。
提案手法が達成したいこと
Heisenberg limitを達成しながら基底状態のエネルギーを推定する手法としてはQuantum Phase Estimation (QPE) が有名ですが、QPEは必要となるancillaの数が多い、回路が深い、逆量子フーリエ変換が必要、といった特徴があるため、計算リソースや実行時間の観点からEarly-FTQCには実行コストが大きいことが知られています。また論文[1]内ではその他の既存手法もEarly-FTQCには不向きであることが指摘されています。具体的には提案手法が達成すべき目標は以下の3つであり、既存手法にこれら3つを満たしているものはありません。以下ではを初期状態とし、ハミルトニアンとしたときはエネルギー固有値に対する固有空間への射影演算子を表しているとします (ただしは昇順にならんでいるとします)。または精度、 は初期状態と基底状態のoverlapを表しています。
1.精度がHeisenberg limitを達成している。つまり合計実行時間が。
2.ancilla qubitは最大で1つ。
3.maximal evolution time (回路実装として要求される時間発展の最大時間)は
提案手法では1つのancilla qubitを持ったシンプルな量子回路が用いられ、古典の後処理を加えることでこの3つの目標を達成します。
提案手法の方針
まず以下のような確率分布を定義します。
ここではを満たすハミルトニアンを正規化するパラメータです。そのためはで値を持ち、各でのみ0でない値をとります。また離散フーリエ変換に対応するようにをとなるように周期で周期化します。
次にの累積分布関数CDF (Cumulative Distribution Function) を考えます。以下のようなHeaviside関数を考えることでからが得られます。ここでは整数 、は畳み込み演算を表しています。
は周期的な関数の畳み込みになっているため通常のCDFの定義とは異なりますが、においては通常の定義と一致することが以下のように確かめられます。
よっては区分的定数関数であり、がの固有値に一致するときにジャンプする関数 (つまり狭義単調増加する階段状の関数)となることが分かります。よってが0からジャンプする点から基底状態のエネルギーが求められることになります。
実際にはCDFを直接得る手法はない (求めたい情報に相当する を知らなければならないため) ので代わりにApproximate CDF (ACDF)を調べることになります。ACDFを得る方法はこの論文の重要なポイントになるため、それを以下で説明します。
ACDF は以下のようにapproximate Heaviside関数を使いながら定義されます。
また論文内では任意ののときとなることが示されています。
次にの構成方法を説明します。まず軟化子 (mollifier)としてを以下のように定義します。
ここでは次の第一種チェビシェフ多項式であり
です。以下に示すようにをプロットしてみるとデルタ関数のような形をしていることが分かります。
プログラム内で用いたimport文,d、deltaなどの変数の具体的な値は付録[1][2]に載せています(以降も同様)。
def M_d_delta(x, d, delta):
numerator = eval_chebyt(d, (1 + 2 * (np.cos(x) - np.cos(delta)) / (1 + np.cos(delta))))
denominator = simpson(numerator, x)
return numerator / denominator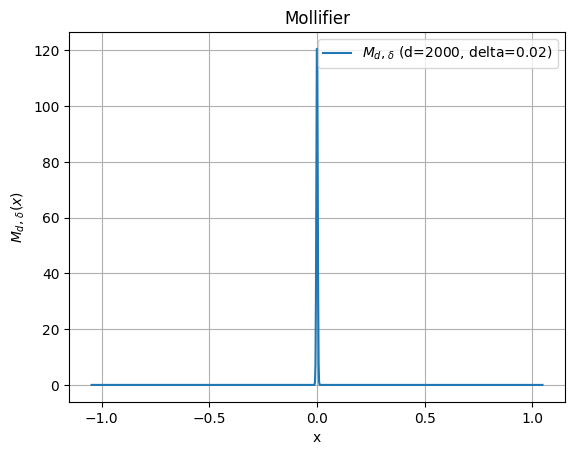
ここでは以下のように定義されます。
ここからをプロットすると以下のようになります。
def H(x):
return 0.5 * (np.sign(x) + 1)
def F(x_vals, d, delta):
x_prime = np.linspace(-np.pi, np.pi, 1000)
F_vals = np.zeros_like(x_vals)
for i, x in enumerate(x_vals):
F_val = simpson(M_d_delta(x_prime, d, delta) * H(x - x_prime), x_prime)
F_vals[i] = F_val
return F_vals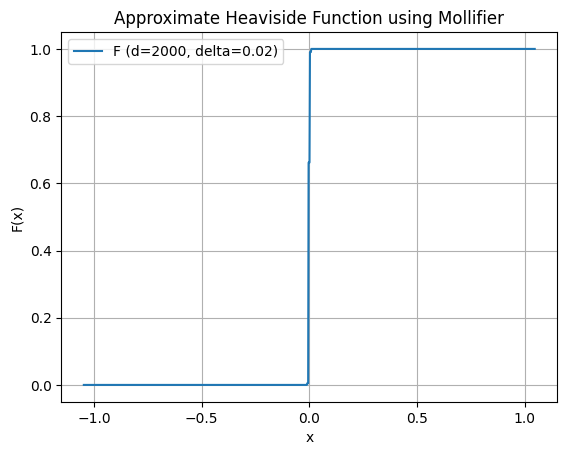
また、、のフーリエ係数が以下のように得られるとします。
はとの畳み込みで定義されているのでとしたとき
が成立します。これを用いてをプロットすると以下のようになります。
def M_d_delta_k(x, d, delta, k):
return simpson(M_d_delta(x, d, delta) * np.exp(-1j * k * x), x) / (2 * np.pi)
def H_k(k):
if k % 2 == 0:
return 0
else:
return 2 / (1j* k)
def F_d_delta_k(x, d, delta, k):
return M_d_delta_k(x, d, delta, k) * H_k(k)
def test_F(x, d, delta):
ret_val = 0
for i in range(-d, d+1):
ret_val += F_d_delta_k(x, d, delta, i)*np.exp(1j * i * x)
return ret_val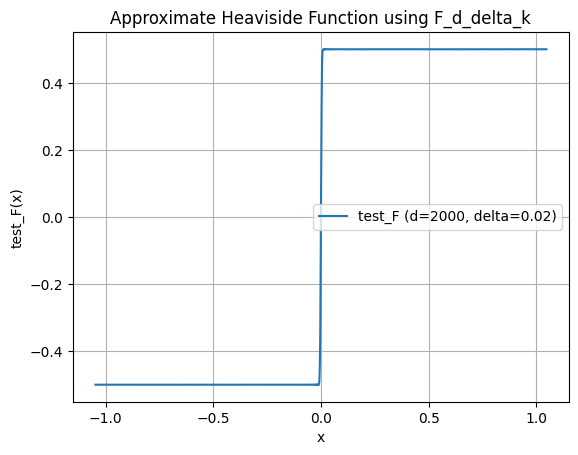
ACDFの評価
ACDF を適切に評価することで基底状態のエネルギーが得られることが分かったので、次にを所望の効率・精度で評価していきましょう。
は次のように変形できます。
ここで以下のようなアダマールテストで用いられる量子回路を考えます。
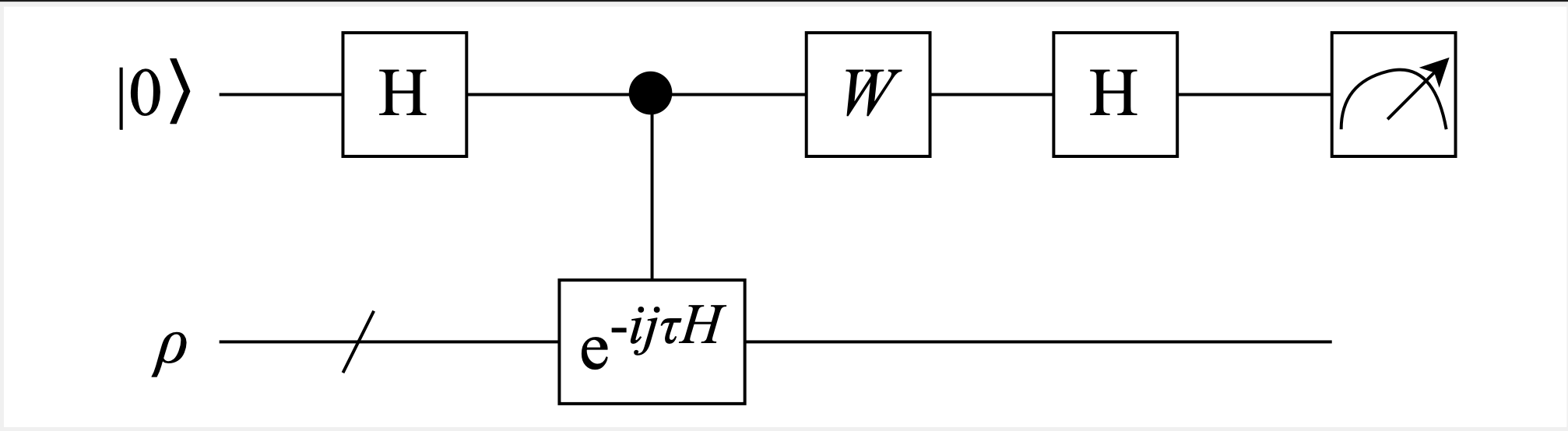
- のとき : 測定結果が0のとき1, 測定結果が1のとき-1となる変数を導入すると
- のとき : 測定結果が0のとき1、測定結果が1のとき-1となる変数を導入すると
が成り立ちます。ここでとなるため、モンテカルロサンプリングを用いることでを評価できると考えられます。論文内では不偏マルチレベルモンテカルロ法と呼ばれる手法を用いることで所望の効率と精度を得ることができることが示されています。以下でその具体的な手法を説明します。
まず以下の確率分布に従うランダム変数を定義します。
ここでは正規化因子です。更に確率変数 を導入します。ここで、です。この確率変数について、に関する平均をとると、以下のように に比例する量になることがわかります。
よって、の不偏推定を以下のように定義できます。
これより、は個のサンプル によっての平均を求めることで推定でき、その推定値 は、
となります。まとめると手順は以下のとおりです。
1.古典コンピュータで を生成する
2. を用いて量子コンピュータを用いたアダマールテストにより を測定する。
3. と を用いて古典コンピュータでACDF の推定値 を求める。
4. の結果について後処理を施し、基底状態のエネルギーを推定する。
以下にプログラムを示します。
1.古典コンピュータで を生成する。
def sample_J(N_s, x, d, delta):
abs_F_j = list()
for i in range(-d, d+1):
abs_F_j.append(np.abs(F_d_delta_k(x, d, delta, i)))
probabilities = abs_F_j / np.sum(abs_F_j)
random_gen = np.random.default_rng()
sample = random_gen.multinomial(N_s, pvals=np.abs(probabilities))
js_counter = Counter({i: c for i, c in enumerate(sample) if c > 0})
samples_phase = dict()
for idx, cnt in js_counter.items():
samples_phase[idx] = np.angle(F_d_delta_k(x, d, delta, idx-d))
return js_counter, samples_phase, np.sum(abs_F_j)# js_counterはJ, samples_phaseは\theta_J, sum_Fは\mathcal{F}
js_counter, samples_phase, sum_F = sample_J(N_s, x, d, delta)
# サンプルしてきた値をファイルに保存
with open('js.pkl', 'wb') as file:
pickle.dump(js_counter, file)
with open('samples_phase.json', 'w') as file:
json.dump(samples_phase, file, indent=4)
with open('sum_F.csv', 'w', newline='') as file:
writer = csv.writer(file)
writer.writerow([sum_F])2. を用いて量子コンピュータを用いたアダマールテストにより を測定する。
ハミルトニアン(hamiltonian)と回路の初期状態 (hf_state)の生成に関しては、付録を参照してください。今回のシミュレーションには水素分子を用いています。
量子回路生成用の関数定義は以下の通りです。
def construct_hadamard_circuit(
time_evolution_circuit: QuantumCircuit,
test_real: bool,
) -> QuantumCircuit:
circuit = QuantumCircuit(time_evolution_circuit.qubit_count)
circuit.add_H_gate(0)
circuit += time_evolution_circuit
if not test_real:
circuit.add_Sdag_gate(0)
circuit.add_H_gate(0)
return circuit
def construct_time_evo_circuit(
evolution_time: float,
n_qubits: int,
hamiltonian_matrix: np.ndarray,
)->NonParametricQuantumCircuit:
circuit = QuantumCircuit(n_qubits+1)
time_evo = expm(-1j * evolution_time * hamiltonian_matrix)
unitary = np.kron(
np.eye(2**n_qubits, dtype=np.complex128),
np.array([[1, 0], [0, 0]], dtype=np.complex128),
)
unitary += np.kron(time_evo, np.array([[0, 0], [0, 1]], dtype=np.complex128))
circuit.add_UnitaryMatrix_gate(range(n_qubits + 1), unitary.tolist())
return circuit
本実装では、NumPyの行列を量子ゲート化する add_UnitaryMatrix_gate を用いていることに注意してください。このゲートはqulacsなどのシミュレータでは実行可能なものの、実際の量子コンピュータでは実行できません。量子コンピュータで動かしたい場合は、量子コンピュータで実行可能なゲートに分解していく工夫が必要になりますが、ここでは割愛します。
量子回路の出力結果サンプリングの関数定義は以下の通りです。
def hadamard_test(real_circuit: NonParametricQuantumCircuit, imag_circuit: NonParametricQuantumCircuit, sampler: Sampler, cnt, n_qubits):
real_cnt = sampler(apply_circuit(real_circuit, quantum_state(n_qubits+1, bits=hf_state.bits<<1)).circuit, shots=cnt)
imag_cnt = sampler(apply_circuit(imag_circuit, quantum_state(n_qubits+1, bits=hf_state.bits<<1)).circuit, shots=cnt)
real_cnt = get_hadamard_test_ancilla_qubit_counter(real_cnt)
imag_cnt = get_hadamard_test_ancilla_qubit_counter(imag_cnt)
real = get_expectation_val_from_hadamard_counter(real_cnt)
imag = get_expectation_val_from_hadamard_counter(imag_cnt)
return real + 1j * imag
def get_hadamard_test_ancilla_qubit_counter(
cnt: Counter[int]
) -> Counter[int]:
hadamard_cnt = Counter()
for c in cnt:
hadamard_cnt += Counter({c % 2: cnt[c]})
return hadamard_cnt
def get_expectation_val_from_hadamard_counter(
hadamard_cnt: Counter[int],
) -> float:
return (hadamard_cnt[0] - hadamard_cnt[1]) / sum(hadamard_cnt.values())以上で定義した関数を用いてを生成し、ファイルに値を保存します。ファイル入出力系の関数の具体的な実装は付録を参照してください。
d = 2000
tau = np.pi/(4.0 * np.linalg.norm(hamiltonian_matrix, ord=2))
FZe: dict[int, complex] = {}
js_file = load_pickle_file('js.pkl')
samples_phase_file = load_json_file('samples_phase.json')
sum_F_file = read_csv_to_float_list('sum_F.csv')
for idx, cnt in js_file.items():
print(idx, cnt)
k = idx - d
phase = samples_phase_file[str(idx)]
evolution_time = k * tau
real_circ = construct_hadamard_circuit(construct_time_evo_circuit(evolution_time, n_qubits, hamiltonian_matrix), True)
imag_circ = construct_hadamard_circuit(construct_time_evo_circuit(evolution_time, n_qubits, hamiltonian_matrix), False)
z = hadamard_test(real_circ, imag_circ, sampler, cnt, n_qubits)
FZe[k] = sum_F_file[0] * z * np.exp(1j*phase) * cnt / N_s
save_complex_list_to_file(FZe, 'FZe.json')3. と を用いて古典コンピュータでACDF の推定値 を求める。
の関数定義(cdf)は以下のとおりです。
def cdf(x: float, FZe_file) -> float:
return sum([z * np.exp(1j*k*x) for k, z in FZe_file.items()])これを用いてACDF を取得し、プロットすると以下のような結果が得られます。
FZe_file = load_complex_list_from_json_file("FZe.json")
acdf = [cdf(x_val, FZe_file) for x_val in x]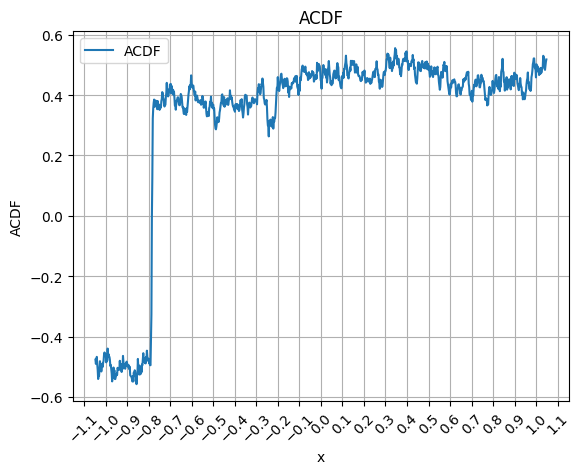
post processing : 基底状態エネルギーの推定
4. の結果について後処理を施し、基底状態のエネルギーを推定する。
ここまでの処理によりACDFが得られたことになります。 の定義より、理想的には、ACDF はにおいて0であり、において高さの最初のステップが起こるということが分かります。つまりこのステップが起こるをとしたときが推定すべき基底状態のエネルギーになります。
今回の例ではなので、程度であることが予想されます。
実際に今回使用したハミルトニアンを固有値分解すると
l, p = np.linalg.eigh(hamiltonian_matrix)
print(l)[-1.01546825 -0.87542794 -0.87542794 -0.87542794 -0.68257868 -0.68257868
-0.56415783 -0.56415783 -0.42938376 -0.36802837 -0.36802837 -0.28043638
-0.28043638 -0.26922131 0.17197088 0.37798372]よって実際の基底状態エネルギーは-1.0155である事が分かります。
ここでは の最初のステップを自動的に検出する方法を説明します。
論文内では以下のProblem 1を解くことでの推定が誤差で行えることが示されています。
Problem 1 : 、に対して以下を満たすを見つける。
Problem 1を2分探索likeな方法で解くアルゴリズムINVERT_CDFによってを推定できます。
INVERT_CDFの概要は以下のようになっています。
1.
2.
3.CERTIFY()
#CERTIFY()はProblem 1の1つ目の式が満たされていれば0を、2つ目の式が満たされていれば1を返す。両方が満たされていれば0か1をランダムに返す。
4.が0であればを右にずらす。が1であればを左にずらす。
つまり
if then
else
5.であれば2.に戻る。そうでなければ6.に進む。
6.の推定値として、を出力する。
INVERT_CDFのプログラムは以下のようになります。
def certify(x: float, FZe_file) -> bool:
b, c = 0, 0
cutoff = 0.75 * eta - 0.5
print(f"cutoff: {cutoff}")
for i in range(n_batch):
print(f"running batch {i}")
y = cdf(x, FZe_file).real
print(f"cdf({x}) = {y}")
if y > cutoff:
c += 1
if c <= n_batch//2:
b += 1
print(f"certify result: {b}")
return bool(b)
def invert_cdf(FZe_file):
x0, x1 = -np.pi/3, np.pi/3
cnt = 0
while x1 - x0 > 1e-3:
cnt += 1
print("----------------------------------------------")
print(f"Iteration: {cnt}")
print(f"Searching between [{x0}, {x1}]")
curr_x = (x0 + x1)/2
print(f"Current x [{curr_x}]")
if certify(curr_x, FZe_file):
x0 = curr_x - 2 * delta/3
else:
x1 = curr_x + 2 * delta/3
next_x = (x0 + x1)/2
if abs(curr_x - next_x) < 1e-6:
break
print("----------------------------------------------")
print("The ground state energy is", (x0 + x1)/2/tau)
return (x0 + x1)/2実行結果は以下のとおりです。
----------------------------------------------
Iteration: 1
Searching between [-1.0471975511965976, 1.0471975511965976]
Current x [0.0]
cutoff: -0.050000000000000044
running batch 0
cdf(0.0) = 0.44451311653617664
certify result: 0
----------------------------------------------
Iteration: 2
Searching between [-1.0471975511965976, 0.013333333333333334]
Current x [-0.5169321089316321]
cutoff: -0.050000000000000044
running batch 0
cdf(-0.5169321089316321) = 0.3601542183548748
certify result: 0
----------------------------------------------
Iteration: 3
Searching between [-1.0471975511965976, -0.5035987755982988]
Current x [-0.7753981633974483]
cutoff: -0.050000000000000044
running batch 0
cdf(-0.7753981633974483) = 0.3813951990897186
certify result: 0
----------------------------------------------
...
cdf(-0.7854570267994726) = -0.049966381962948336
certify result: 0
----------------------------------------------
The ground state energy is -1.0155456305957278
これより後処理によって固有値は -1.0156 であると読み取ることができました。一方で、ハミルトニアンを直接的に数値対角化して求めれらた固有値は -1.0155 でした。後処理によって得られた値は、かなり正確に求められていることが分かります。
付録 : プログラムの補足
付録1:import文一覧
import csv
import json
import pickle
from collections import Counter
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import MultipleLocator
from pyscf import gto, scf
from quri_parts.circuit import NonParametricQuantumCircuit, QuantumCircuit
from quri_parts.core.operator import get_sparse_matrix
from quri_parts.core.sampling import Sampler
from quri_parts.core.state import apply_circuit, quantum_state
from quri_parts.openfermion.mol import get_qubit_mapped_hamiltonian
from quri_parts.pyscf.mol import get_spin_mo_integrals_from_mole
from quri_parts.qulacs.sampler import create_qulacs_vector_sampler
from scipy.integrate import simpson
from scipy.linalg import expm
from scipy.special import eval_chebyt付録2:変数定義
x_low = -np.pi/3
x_high = np.pi/3
delta = 0.02
d = 2000
N_s = 3000
x = np.linspace(x_low, x_high, 1000)
eta = 0.6
n_batch = 1
## Constructing the Hamiltonian and initial state(hf_state)
mole = gto.M(atom="H 0 0 0; H 0 0 1.4")
mf = scf.RHF(mole).run(verbose=0)
hamiltonian, jw_mapping = get_qubit_mapped_hamiltonian(
*get_spin_mo_integrals_from_mole(mole, mf.mo_coeff)
)
hamiltonian_matrix = get_sparse_matrix(hamiltonian).toarray()
state_mapper = jw_mapping.state_mapper
hf_state = state_mapper([i for i in range(jw_mapping.n_fermions)])
sampler = create_qulacs_vector_sampler()
tau = np.pi/(4.0 * np.linalg.norm(hamiltonian_matrix, ord=2))
dim = hamiltonian_matrix.shape[0]
n_qubits = int(np.log2(dim))付録3:ファイル入出力用の関数定義
def read_csv_to_int_list(file_path):
with open(file_path, 'r') as file:
reader = csv.reader(file)
for row in reader:
return [int(value) for value in row]
def read_csv_to_float_list(file_path):
with open(file_path, 'r') as file:
reader = csv.reader(file)
for row in reader:
return [float(value) for value in row]
class ComplexEncoder(json.JSONEncoder):
def default(self, obj):
if isinstance(obj, (np.complex128, complex)):
return {'real': obj.real, 'imag': obj.imag}
return json.JSONEncoder.default(self, obj)
def save_complex_list_to_file(complex_list, filename):
with open(filename, 'w') as f:
json.dump(complex_list, f, cls=ComplexEncoder, indent=4)
def load_complex_list_from_json_file(filename):
with open(filename, 'r') as f:
data = json.load(f)
complex_dict = {}
for key, value in data.items():
real = value['real']
imag = value['imag']
complex_dict[int(key)] = complex(real, imag)
return complex_dict
def load_pickle_file(filename):
with open(filename, 'rb') as file:
loaded_counter = pickle.load(file)
return loaded_counter
def load_json_file(filename):
with open(filename, 'r') as file:
loaded_data = json.load(file)
return loaded_data
参考文献
[1] L. Lin et al. Heisenberg-Limited Ground-State Energy Estimation for Early Fault-Tolerant Quantum Computers. PRXQuantum. 2022.
[2]QunaSys. QURI Parts. https://github.com/QunaSys/quri-parts.
執筆者 : 柚木隼人

 QunaSys Tech Blog
QunaSys Tech Blog